题目内容
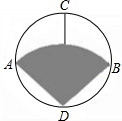 某种商品的商标图案如图(图中的阴影部分),已知⊙O的直径AB⊥CD,且AB=8cm,弧AB是以D为圆心,DA为半径的弧,则商标图案的面积为
某种商品的商标图案如图(图中的阴影部分),已知⊙O的直径AB⊥CD,且AB=8cm,弧AB是以D为圆心,DA为半径的弧,则商标图案的面积为分析:从图中可以看出阴影部分的面积是一个扇形,而且从给出的条件中可以得知,这个扇形的圆心角是90度,半径可以解直角三角形得出.然后根据扇形的面积公式计算即可.
解答:解:∵AB是直径
∴∠ADB=90°
∵AB=8,直径AB⊥CD
∴AD=BD
根据勾股定理可得:2AD2=64
解得:AD=4
cm
根据扇形的面积公式得:
商标图案的面积=
=8πcm2.
∴∠ADB=90°
∵AB=8,直径AB⊥CD
∴AD=BD
根据勾股定理可得:2AD2=64
解得:AD=4
| 2 |
根据扇形的面积公式得:
商标图案的面积=
| 90π×32 |
| 360 |
点评:本题的关键是计算出扇形的圆心角和半径,利用扇形公式计算面积.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
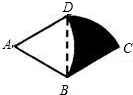 某种商品的商标图案如图所示(阴影部分),已知菱形ABCD的边长为4,∠A=60°,
某种商品的商标图案如图所示(阴影部分),已知菱形ABCD的边长为4,∠A=60°,

 是以A为圆心,AB长为半径的弧,
是以A为圆心,AB长为半径的弧, 是以B为圆心,BC长为半径的弧,则该商标图案的面积为______
是以B为圆心,BC长为半径的弧,则该商标图案的面积为______
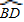 是以A为圆心,AB长为半径的弧,
是以A为圆心,AB长为半径的弧, 是以B为圆心,BC长为半径的弧,则该商标图案的面积为______
是以B为圆心,BC长为半径的弧,则该商标图案的面积为______