题目内容
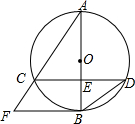 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=| 3 | 4 |
(1)求⊙O的半径长;
(2)求线段CF长.
分析:(1)过O作OH垂直于AC,利用垂径定理得到H为AC中点,求出AH的长为4,根据同弧所对的圆周角相等得到tanA=tan∠BDC,求出OH的长,利用勾股定理即可求出圆的半径OA的长;
(2)由AB垂直于CD得到E为CD的中点,得到EC=ED,在直角三角形AEC中,由AC的长以及tanA的值求出CE与AE的长,由FB为圆的切线得到AB垂直于BF,得到CE与FB平行,由平行得比例列出关系式求出AF的长,根据AF-AC即可求出CF的长.
(2)由AB垂直于CD得到E为CD的中点,得到EC=ED,在直角三角形AEC中,由AC的长以及tanA的值求出CE与AE的长,由FB为圆的切线得到AB垂直于BF,得到CE与FB平行,由平行得比例列出关系式求出AF的长,根据AF-AC即可求出CF的长.
解答: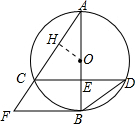 解:(1)作OH⊥AC于H,则AH=
解:(1)作OH⊥AC于H,则AH=
AC=4,
在Rt△AOH中,AH=4,tanA=tan∠BDC=
,
∴OH=3,
∴半径OA=
=5;
(2)∵AB⊥CD,
∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA=
,
设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=
,
则CE=DE=
,AE=
,
∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴
=
,即
=
,
解得:AF=
,
则CF=AF-AC=
.
 解:(1)作OH⊥AC于H,则AH=
解:(1)作OH⊥AC于H,则AH=| 1 |
| 2 |
在Rt△AOH中,AH=4,tanA=tan∠BDC=
| 3 |
| 4 |
∴OH=3,
∴半径OA=
| AH2+OH2 |
(2)∵AB⊥CD,
∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA=
| 3 |
| 4 |
设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=
| 8 |
| 5 |
则CE=DE=
| 24 |
| 5 |
| 32 |
| 5 |
∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴
| AC |
| AF |
| AE |
| AB |
| 8 |
| AF |
| ||
| 10 |
解得:AF=
| 25 |
| 2 |
则CF=AF-AC=
| 9 |
| 2 |
点评:此题考查了切线的性质,垂径定理,锐角三角函数定义,勾股定理,以及平行线的性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( ) 如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
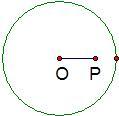 22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有
22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有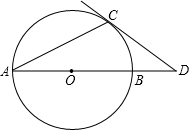 如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )
如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )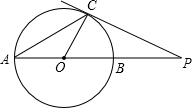 (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )