题目内容
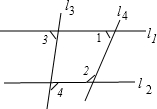 如图,∠1与∠3互余,∠2与∠3的余角互补,∠4=115°,则∠3为
如图,∠1与∠3互余,∠2与∠3的余角互补,∠4=115°,则∠3为
- A.45°
- B.60°
- C.65°
- D.70°
C
分析:∠1与∠3互余,∠2与∠3的余角互补,则可以知道∠1+∠3=90°,∠2+(90°-∠3)=180°,即∠2-∠3=90°,所以∠1+∠2=180°,则l1∥l2,就可以根据平行线的性质求得∠3的大小.
解答: 解:∵∠1与∠3互余,∠2与∠3的余角互补,
解:∵∠1与∠3互余,∠2与∠3的余角互补,
∴∠1+∠3=90°,∠2+(90°-∠3)=180°,
∴∠1+∠2=180°,
∴l1∥l2,
∴∠3+∠5=180°,
又∵∠5=∠4=115°,
∴∠3=180°-115°=65°.
故选C.
点评:解决本题的关键是由已知条件能够联想到l1∥l2,由已知条件进行合理的推理是学习数学所要达到的要求.
分析:∠1与∠3互余,∠2与∠3的余角互补,则可以知道∠1+∠3=90°,∠2+(90°-∠3)=180°,即∠2-∠3=90°,所以∠1+∠2=180°,则l1∥l2,就可以根据平行线的性质求得∠3的大小.
解答:
 解:∵∠1与∠3互余,∠2与∠3的余角互补,
解:∵∠1与∠3互余,∠2与∠3的余角互补,∴∠1+∠3=90°,∠2+(90°-∠3)=180°,
∴∠1+∠2=180°,
∴l1∥l2,
∴∠3+∠5=180°,
又∵∠5=∠4=115°,
∴∠3=180°-115°=65°.
故选C.
点评:解决本题的关键是由已知条件能够联想到l1∥l2,由已知条件进行合理的推理是学习数学所要达到的要求.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
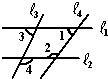 4、如图,∠1与∠3互余,∠2与∠3的余角互补,∠4=115°,则∠3为( )
4、如图,∠1与∠3互余,∠2与∠3的余角互补,∠4=115°,则∠3为( )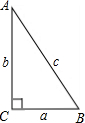 我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA=
我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA= 如图,∠AOE与∠BOF互余,那么AO与BO是否垂直?试说明理由.
如图,∠AOE与∠BOF互余,那么AO与BO是否垂直?试说明理由. 如图,∠AOC与∠COB互余,∠COD:∠COB=1:2,若∠AOC=38°,则∠BOD等于( )
如图,∠AOC与∠COB互余,∠COD:∠COB=1:2,若∠AOC=38°,则∠BOD等于( ) 如图,∠ABP与∠PBC互余,∠CBD=30°,BP平分∠ABD,则∠ABP=
如图,∠ABP与∠PBC互余,∠CBD=30°,BP平分∠ABD,则∠ABP=