题目内容
如图，∠AOE与∠BOF互余，那么AO与BO是否垂直？试说明理由．分析：根据平角的定义求得∠AOB=90°．则由垂直的定义证得AO与BO垂直．
解答：解：AO与BO垂直．理由如下：
∵∠AOE与∠BOF互余，
∴∠AOE+∠BOF=90°，
又∵∠AOE+∠AOB+∠BOF=180°，
∴∠AOB=90°，
∴AO⊥BO，即AO与BO垂直．
∵∠AOE与∠BOF互余，
∴∠AOE+∠BOF=90°，
又∵∠AOE+∠AOB+∠BOF=180°，
∴∠AOB=90°，
∴AO⊥BO，即AO与BO垂直．
点评：本题考查了垂直的定义．当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．
练习册系列答案
相关题目
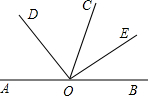如图，∠AOC与∠BOC是邻补角，OD，OE分别是∠AOC，∠BOC的平分线．
如图直线AB与CO相交于点O，∠AOE=90°，图中∠1和∠2的关系是（ ）
如图，∠AOC与∠BOC是邻补角，OD，OE分别是∠AOC，∠BOC的平分线．
如图，∠AOE与∠BOF互余，那么AO与BO是否垂直？试说明理由．