Question

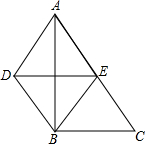如图，Rt△ABC中，∠B=90°，过点B作DB∥AC，且DB=

1

2

AC，连接AD、ED，E是AC的中点．
（1）求证：DE∥BC；
（2）请问四边形ADBE是特殊四边形吗？试做出判断，并说明理由．

Answer 1

分析：（1）推出CE=BD，CE∥BD，得出平行四边形BDEC，根据平行四边形的性质推出即可；
（2）求出BDF=AE，BD∥AE，得出平行四边形ADBE，根据DE∥BC，∠ABC=90°推出DE⊥AB，根据菱形的判定推出即可、

解答：（1）证明：∵E是AC的中点，
∴CE=AE=

1

2

AC，
∵DB=

1

2

AC，
∵BD=CE，
∵BD∥AC，
∴BD∥CE，
∴四边形BDEC是平行四边形，
∴DE∥BC．

（2）解：四边形ADBE是菱形，
理由是：∵DE∥BC，∠ABC=90°，
∴DE⊥AB，
∵AE=

1

2

AC，DB=

1

2

AC，BD∥AC，
∴BD=AE，BD∥AE，
∴四边形ADBE是平行四边形，
∴平行四边形ADBE是菱形．

点评：本题考查了平行四边形的性质和判定，菱形的判定等知识点，注意：有一组对边平行且相等的四边形是平行四边形，对角线互相垂直的平行四边形是菱形．