题目内容
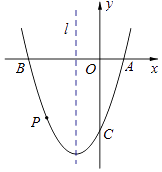
【题目】如图，抛物线y= 
x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A、B，且B点的坐标为（2，0）．
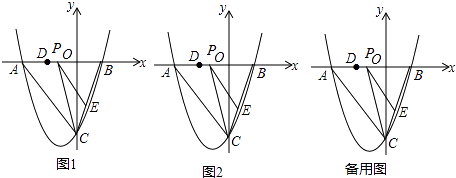
（1）求抛物线的解析式；
（2）若点P是AB上的一个动点，过点P作PE∥AC交BC于点E，连接CP，求△PCE面积最大时P点的坐标；
（3）在（2）的条件下，若点D为OA的中点，点M是线段AC上一点，当△OMD为等腰三角形时，连接MP、ME，把△MPE沿着PE翻折，点M的对应点为点N，直接写出点N的坐标．
【答案】
（1）
解：根据题意得：
，
解得： 
，
所以该抛物线的解析式为：y= 
x2+x﹣4；
（2）
解：令y=0，即 x2+x﹣4=0，解得x1=﹣4，x2=2，
∴A（﹣4，0），S△ABC= ABOC=12
设P点坐标为（x，0），则PB=2﹣x．
∵PE∥BC，
∴∠BPE=∠BAC，∠BEP=∠BCA，
∴△PBE∽△BAC，
∴ 
=（ 
）2，即 
=（ 
）2，
化简得：S△PBE= 
（2﹣x）2．
S△PCE=S△PCB﹣S△PBE= PBOC﹣S△PBE= ×（2﹣x）×4﹣ （2﹣x）2
=﹣ x2﹣ 
x+ 
=﹣ （x+1）2+3
∴当x=﹣1时，S△PCE的最大值为3．
（3）
解：由（2）已知A（﹣4，0），
∵点D为0A中点，
∴D（﹣2，0），
设直线AC的解析式为y=mx+n，
把A（﹣4，0）、C（0，﹣4）分别代入得：
，解得 
，
∴直线AC的解析式为y=﹣x﹣4．
∵PE∥AC，所以可设直线PE的解析式为y=﹣x+a，
将P（﹣1，0）代入y=﹣x﹣a得a=﹣1，
所以直线PE的解析式为y=﹣x﹣1．
设直线BC的解析式为y=kx+a′，
将B（2，0）、C（0，﹣4）代入y=kx+a′得 
，
解得k=2，a′=﹣4．
所以直线BC的解析式为y=2x﹣4．
由2x﹣4=﹣x﹣1得x=1，将x=1代入y=2x﹣4得y=﹣2，
∴E点坐标为（1，﹣2）．
①当MD=OD时，如图1：
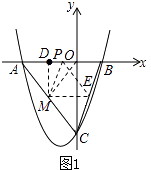
∵AD=MD=AD，OA=OC，∠DAM=∠OAC，
∴△ADM∽△AOC，
∴∠ADM=∠AOC=90°，即DM⊥x轴，
<>∴M的横坐标为﹣2，将x=﹣2代入y=﹣x﹣4，得y=﹣2．所以此时M的坐标为（﹣2，﹣2）；
∵M和E点纵坐标相等，
∴ME∥x轴，
∴∠PEM=45°．
由翻折得∠ENM=2∠PEM=90°，即NE∥y轴，
∴EN=ME=3，
∵E（1，﹣2），
∴N（1，1）．
②当DM=OM时，过点M作MG⊥x轴交于点，如图2：
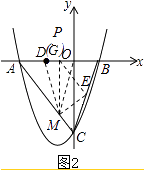
易知DG=OG=1，即G点与P点重合，M的横坐标为﹣1，
将x=﹣1代入y=﹣x﹣4，得y=﹣3．
∴M（﹣1，﹣3）．
∵ME= 
= 
，EB= 
= ，
∴ME=EB，
∵PB=3，PM=3，即PB=PM，
又∵PE=PE，
∴△BPE≌△MPE，
∴∠BEP=∠MEP，
∴点N与点B重合，
∴N（2，0）；
③当OD=OM时，
设点O到AC的最短距离为h，则OAOC=hAC
∵AC= 
= 
=4 
，
∴h= 
=2 ，
∵h＞OD，
∴OD≠OM．此时等腰△OMD不存在．
综上所述，N点的坐标分别为（1，1）或（2，0）．
【解析】（1）把B点和C点坐标分别代入y= x2+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；（2）首先求出△PCE面积的表达式，然后利用二次函数的性质求出其最大值；（3）易知D（﹣2，0），接着利用待定系数求出直线AC的解析式为y=﹣x﹣4，再根据直线PE与直线BC的解析式求得点E的坐标为（1，﹣2）．求M点分类讨论：①当MD=OD时，求得M的坐标为（﹣2，﹣2）；所以ME∥x轴，则∠PEM=45°，由翻折得∠NEM=90°，所以NE∥y轴，可得N（1，1）；②当DM=OM时，求得M的坐标为（﹣1，﹣3），又可证得△MPE≌△BPE，所以N与B重合，N点坐标为（2，0）；③OD=OM时，等腰△OMD不存在．
【考点精析】本题主要考查了相似三角形的应用的相关知识点，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能正确解答此题．
