题目内容
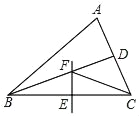
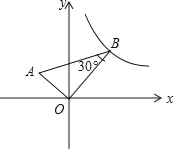
【题目】如图，△AOB中，∠O=90°，AO=8cm，BO=6cm，点C从A点出发，在边AO上以4cm/s的速度向O点运动，与此同时，点D从点B出发，在边BO上以3cm/s的速度向O点运动，过OC的中点E作CD的垂线EF，则当点C运动了________s时，以C点为圆心，2cm为半径的圆与直线EF相切．
【答案】
【解析】
当以点C为圆心，2cm为半径的圆与直线EF相切时，即CF=2cm，又因为∠EFC=∠O=90°，所以△EFC∽△DOC，利用对应边的比相等即可求出EF的长度，再利用勾股定理列出方程即可求出t的值，要注意t的取值范围为0≤t≤2．
当以点C为圆心，2cm为半径的圆与直线EF相切时，
此时，CF=2，
由题意得：AC=4t，BD=3t
∴OC=8-4t，OD=6-3t，
∵点E是OC的中点，
∴CE=
OC=4-2t，
∵∠EFC=∠O=90°，∠FCE=∠DCO，
∴△EFC∽△DOC，
∴
，
∴EF=
，
由勾股定理可知：CE2=CF2+EF2，
∴（4-2t）2=2 2+（
）2，
解得：t=或t=
，
∵0≤t≤2，
∴t=．
故答案为：．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了了解学生学习的环境（教室），研究人员对某校一间（坐满学生、门窗关闭）教室中的
的总量进行检测，得到的部分数据如下：
教室连续使用时间 |
|
|
|
|
|
|
|
|
|
|
|
经研究发现，该教室空气中总量
是教室连使用时间
的一次函数．
（1）请直接写出
与的函数关系式；
（2）根据有关资料推算，当该教室空气中总量达到
时，学生将会稍感不适，则该教室连续使用__________
学生将会开始稍感不适．
（3）如果该教室在连续使用
分钟时开门通风，在学生全部离开教室的情况下，
分钟可将教室空气中的总量减少到
，求开门通风时教室空气中平均每分钟减少多少立方米？
