题目内容
20、如图1,E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点,每组对边上的两个点,可以连接成一条线段.
(1)如图2,如果EF∥BC,MN∥CD,那么EF
(2)如图3,如果E与A,F与C,M与B,N与D重合,那么EF
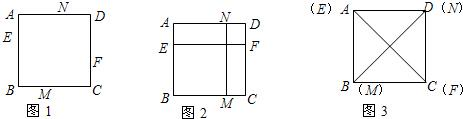
(3)当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想.
(1)如图2,如果EF∥BC,MN∥CD,那么EF
垂直
MN(位置),EF等于
MN(大小);(2)如图3,如果E与A,F与C,M与B,N与D重合,那么EF
垂直
MN(位置),EF等于
MN(大小);
(3)当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想.
分析:(1)由EF∥BC,MN∥CD,BC⊥CD可得EF⊥MN,且EF=MN.
(2)E与A,F与C,M与B,N与D重合,则EF,MN是正方形的对角线,根据对角线的性质互相垂直且互相平分可得出结论.
(2)E与A,F与C,M与B,N与D重合,则EF,MN是正方形的对角线,根据对角线的性质互相垂直且互相平分可得出结论.
解答:解:(1)EF⊥MN,EF=MN;
(2)EF⊥MN,EF=MN;
(3)猜想:当EF⊥MN时,才会有EF=MN,如图,连接EF交MN与O,作EF⊥MN.
证明猜想:如图,作EF⊥MN,EF交MN与O.
过点N作NG⊥BC,过点F作FH⊥AB交MN与U,
又EF⊥MN,在Rt△MNG和Rt△EFH中,∠MGN=∠EHF=90°,FH=NG,
∠MNG+∠NUF=90°,∠EFH++∠NUF=90°
∴∠MNG=∠EFH
所以Rt△MNG≌Rt△EFH,所以EF=MN.
(2)EF⊥MN,EF=MN;
(3)猜想:当EF⊥MN时,才会有EF=MN,如图,连接EF交MN与O,作EF⊥MN.
证明猜想:如图,作EF⊥MN,EF交MN与O.
过点N作NG⊥BC,过点F作FH⊥AB交MN与U,
又EF⊥MN,在Rt△MNG和Rt△EFH中,∠MGN=∠EHF=90°,FH=NG,
∠MNG+∠NUF=90°,∠EFH++∠NUF=90°
∴∠MNG=∠EFH
所以Rt△MNG≌Rt△EFH,所以EF=MN.
点评:本题考查正方形的性质和全等三角形的判定,要根据平时做题的结论做出大胆的猜想,然后再去证明.

练习册系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.