题目内容
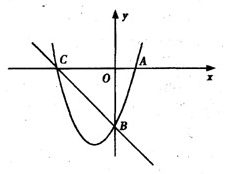
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数解析式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.


【解析】(1)根据题意,y=ax2+bx+c的对称轴为x=1,且过A(-1,0),C(0,-3),可得
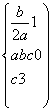 解得
解得![]()
∴抛物线所对应的函数解析式为y=x2-2x-3.
(2)由y=x2-2x-3可得,抛物线与x轴的另一交点B(3,0)如图①,连接BC,交对称轴x=1于点M.因为点M在对称轴上,MA=MB.所以直线BC与对称轴x=1的交点即为所求的M点.
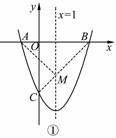

设直线BC的函数关系式为y=kx+b,由B(3,0),C(0,-3),解得y=x-3,由x=1,解得y=-2.
故当点M的坐标为(1,-2)时,点M到点A的距离与到点C的距离之和最小.
(3)如图②,设此时点P的坐标为(1,m),抛物线的对称轴交x轴于点F(1,0).连接PC、PB,作PD垂直y轴于点D,则D(0,m).
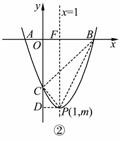

在Rt△CDP中,
CD=|m-(-3)|=|m+3|,DP=1,
∴CP2=CD2+DP2=(m+3)2+1.
在Rt△PFB中,PF=|m|,FB=3-1=2,
∴PB2=PF2+FB2=m2+4.
在Rt△COB中,CB2=OB2+OC2=32+32=18.
当∠PCB=90°时,有CP2+CB2=PB2.
即(m+3)2+1+18=m2+4.解得m=-4.
∴使∠PCB=90°的点P的坐标为(1,-4).

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目