题目内容
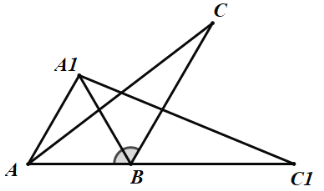
【题目】如图，在四边形ABCD中，AB∥CD，∠BAD、∠ADC的平分线AE、DF分别与线段BC相交于点E、F，∠DFC=30°，AE与DF相交干点G，则∠AEC=________.
【答案】120°
【解析】
根据平行线的性质得到∠BAD+∠ADC=180°；然后根据角平分线的定义，推知∠DAE+∠ADF=90°，即可得到∠AGD=90°，根据对顶角相等可得∠AGD=∠FGE，再根据外角定理即可求出∠AEC.
解：：∵AB∥DC，
∴∠BAD+∠ADC=180°．
∵AE，DF分别是∠BAD，∠ADC的平分线，
∴
，
∴
，
∴∠AGD=90°，
又∵∠AGD和∠FGE是对顶角，
∴∠AGD=∠FGE=90°，
∴∠AEC=∠FGE+∠∠DFC=90°+30°=120°.
练习册系列答案
相关题目
