题目内容
【题目】已知二次函数y=x2﹣4x+3.
(1)把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)写出二次函数的对称轴和顶点坐标;
(3)求二次函数与x轴的交点坐标;
(4)画出这个二次函数的图象;
(5)观察图象并写出y随x增大而减小时自变量x的取值范围.
(6)观察图象并写出当x为何值时,y>0.
【答案】(1)y=(x﹣2)2﹣1;(2)对称轴是直线x=2,顶点坐标为(2,﹣1);(3)(1,0)(3,0);(4)见解析;(5)当y随x增大而减小时x≤2;(6)当x<1或x>3时,y>0.
【解析】
试题分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)根据(1)中的二次函数解析式直接写出答案;
(3)将已知函数解析式转化为两点式方程即可得到答案;
(4)根据顶点坐标,抛物线与y轴的交点坐标以及抛物线与x轴的交点坐标画出图象;
(5)(6)根据图象写出x的取值范围.
解:(1)y=x2﹣4x+3=(x﹣2)2﹣1,则该抛物线解析式是y=(x﹣2)2﹣1;
(2)由(1)知,该抛物线解析式为:y=(x﹣2)2﹣1,
所以对称轴是直线x=2,顶点坐标为(2,﹣1);
(3)∵二次函数y=x2﹣4x+3=(x﹣1)(x﹣3),
∴二次函数与x轴的交点坐标分别是:(1,0)(3,0);
(4)其图象如图所示:
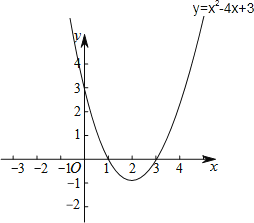
(5)由图象知,当y随x增大而减小时x≤2;
(6)由图象知,当x<1或x>3时,y>0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目