Question

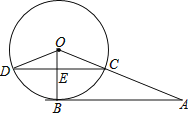
【题目】如图，A为⊙O外一点，AB切⊙O于点B，AO交⊙O于C，CD⊥OB于E，交⊙O于点D，连接OD．若AB=12，AC=8．

（1）求OD的长；

（2）求CD的长．

Answer 1

【答案】（1）5；（2）．

【解析】

试题分析：（1）设⊙O的半径为R，根据切线定理得OB⊥AB，则在Rt△ABO中，利用勾股定理得到R2+122=（R+8）2，解得R=5，即OD的长为5；

（2）根据垂径定理由CD⊥OB得DE=CE，再证明△OEC∽△OBA，利用相似比可计算出CE=，所以CD=2CE=．

解：（1）设⊙O的半径为R，

∵AB切⊙O于点B，

∴OB⊥AB，

在Rt△ABO中，OB=R，AO=OC+AC=R+8，AB=12，

∵OB2+AB2=OA2，

∴R2+122=（R+8）2，

解得R=5，

∴OD的长为5；

（2）∵CD⊥OB，

∴DE=CE，

而OB⊥AB，

∴CE∥AB，

∴△OEC∽△OBA，

∴=，

即=，

∴CE=，

∴CD=2CE=．