题目内容
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的
延长线交线段BC于点P,连AP、AG.
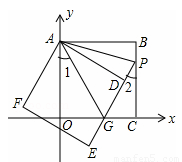
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式.
(1)证明见解析(2)∠PAG =45°,PG=OG+BP,理由见解析(3)y=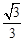 x﹣1
x﹣1
【解析】解:(1)证明:∵∠AOG=∠ADG=90°,
∴在Rt△AOG和Rt△ADG中,AO=AD,AG=AG,
∴△AOG≌△ADG(HL)。
(2)∠PAG =45°,PG=OG+BP。理由如下:
由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP。
∵由(1)△AOG≌△ADG,∴∠1=∠DAG。
又∵∠1+∠DAG+∠DAP+∠BAP=90°,
∴2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°。∴∠PAG=∠DAG+∠DAP=45°。
∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP。
∴PG=DG+DP=OG+BP。
(3)∵△AOG≌△ADG,∴∠AGO=∠AGD。
又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC。
又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°。∴∠1=∠2=30°。
在Rt△AOG中,AO=3,OG=AOtan30°=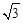 ,
,
∴G点坐标为:(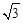 ,0),CG=3﹣
,0),CG=3﹣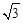 。
。
在Rt△PCG中,PC=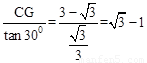 ,∴P点坐标为:(3,
,∴P点坐标为:(3,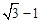 )。
)。
设直线PE的解析式为y=kx+b,
则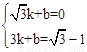 ,解得
,解得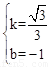 。
。
∴直线PE的解析式为y=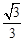 x﹣1。
x﹣1。
(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG。
(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系。
(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式。

 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为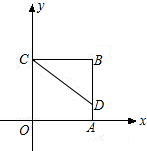 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1. 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是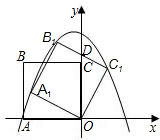 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.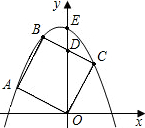 x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为