题目内容
【题目】已知抛物线![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求该抛物线与
,求该抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)若![]() ,
,![]() 且抛物线在
且抛物线在![]() 区间上的最小值是-3,求
区间上的最小值是-3,求![]() 的值.
的值.
【答案】(1)(-1,0),![]() ;(2)b=7或
;(2)b=7或![]() .
.
【解析】
(1)将![]() ,
,![]() ,
,![]() 代入解析式,然后令y=0,求x的值,使问题得解;(2)求得函数的对称轴是x=-b,然后分成-b≤-2,-2<-b≤2和-b>2三种情况进行讨论,然后根据最小值是-3,即可解方程求解.
代入解析式,然后令y=0,求x的值,使问题得解;(2)求得函数的对称轴是x=-b,然后分成-b≤-2,-2<-b≤2和-b>2三种情况进行讨论,然后根据最小值是-3,即可解方程求解.
解:(1)当![]() ,
,![]() ,
,![]() 时
时![]()
当y=0时,![]()
解得:![]()
∴该抛物线与x轴的交点为(-1,0),![]()
(2)当![]() ,
,![]() 时,
时,![]()
∴抛物线的对称轴是x=![]() =-b.
=-b.
当-b≤-2,即b≥2时,在![]() 区间上,y随x增大而增大
区间上,y随x增大而增大
∴当x=-2时,y最小为![]()
解得:b=7;
当-2<-b≤2时,即-2≤b<2,在![]() 区间上
区间上
当x=-b时,y最小为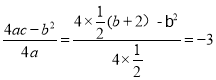
![]()
解得:b=![]() (不合题意)或b=
(不合题意)或b=![]() (不合题意)
(不合题意)
当-b>2,即b<-2时,在![]() 区间上,y随x增大而减小
区间上,y随x增大而减小
∴当x=2时,y最小为![]()
解得:b=![]() .
.
综上,b=7或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目