题目内容
【题目】如图，已知平行四边形ABCD，点O为AD中点，点E在BD上，连接EO并延长交BC于点F，连接BE，DF．
（1）求证：四边形BEDF是平行四边形；
（2）若AB=3
，AD=6，∠BAD=135°，当四边形BEDF为菱形时，求AE的长．
【答案】(1)见解析;(2) AE =1.
【解析】
（1）先根据“SAS”证明△DOE≌△BOF，从而ED=BF，再根据一组对边相等且平行的四边形是平行四边形即可证得结论成立；
（2）过点B作BH⊥AD，交DA延长线于点H，可证△ABH是等腰直角三角形，从而求出BH=HA=3，设AE=x，则EB=ED=6－x，在Rt△BHE中，利用勾股定理列方程求解即可.
（1）证明∵四边形ABCD是平行四边形，
∴BC∥AD，
∴∠ADB=∠CBD，
又∵点O为AD中点，∴BO=OD
∵在△DOE和△BOF中，
，
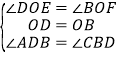∴△DOE≌△BOF，
∴ED=BF，
∴四边形BEDF是平行四边形.
（2）如图，过点B作BH⊥AD，交DA延长线于点H，
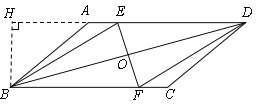
∵∠BAD=135°，
∴∠BAH=45°
在Rt△ABH中，AB=3，
∴BH=HA=3，
设AE=x，
∵四边形BEDF为菱形，
∴EB=ED=6－x
在Rt△BHE中，BH2+HE2=BE2，
∴32+（3+x）2=（6－x）2
解得：x=1 ，
∴AE =1.
练习册系列答案
相关题目
【题目】某城市自来水收费实行阶梯水价，收费标准如下表所示：
月用水量 | 不超过12吨的部分 | 超过12吨的部分且 不超过18吨的部分 | 超过18吨的部分 |
收费标准 | 2元/吨 | 2.5元/吨 | 3元/吨 |
（1）某用户四月份用水量为16吨，需交水费为多少元？
（2）某用户五月份交水费50元，所用水量为多少吨？
（3）某用户六月份用水量为a吨，需要交水费为多少元？
