题目内容
【题目】探究:
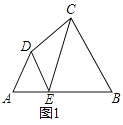
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=![]() ,请直接写出BE、DF与EF之间的数量关系;
,请直接写出BE、DF与EF之间的数量关系;
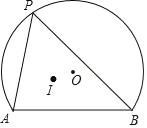
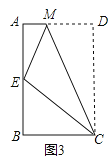
(2)如图2,若把(1)问中的条件变为“四边形ABCD中,AB=AD,∠B+∠D=![]() ,E、F分别是边BC、CD上的点,且
,E、F分别是边BC、CD上的点,且![]() ,则(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
,则(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
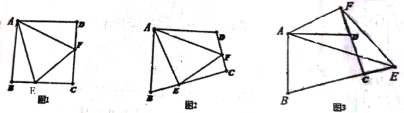
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请写出结论并证明,若不变,请说明理由.
【答案】(1)BE+DF=EF;(2)成立,证明见解析;(3)BE—DF=EF,证明见解析
【解析】
(1)将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF,然后求出∠EAF=∠EAF=45°,利用“边角边”证明△AEF和△AEF′全等,根据全等三角形对应边相等可得EF=EF′,从而得解;
(2)将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,根据旋转变换的性质可得△ADF和△ABF′全等,根据全等三角形对应角相等可得∠BAF′=∠DAF,对应边相等可得AF′=AF,BF′=DF,对应角相等可得∠ABF′=∠D,再根据∠EAF=![]() ∠BAD证明∠EAF′=∠EAF,并证明E、B、F′三点共线,然后利用“边角边”证明△AEF和△AEF′全等,根据全等三角形对应边相等可得EF′=EF,从而得解;
∠BAD证明∠EAF′=∠EAF,并证明E、B、F′三点共线,然后利用“边角边”证明△AEF和△AEF′全等,根据全等三角形对应边相等可得EF′=EF,从而得解;
(3)将△ADF绕点A顺时针旋转,使AD与AB重合,点F落在BC上点F′处,得到△ABF′,根据旋转变换的性质可得△ADF和△ABF′全等,根据全等三角形对应角相等可得∠BAF′=∠DAF,对应边相等可得AF′=AF,BF′=DF,再根据∠EAF=![]() ∠BAD证明∠F′AE=∠FAE,然后利用“边角边"证明△F′AE和△FAE全等,根据全等三角形对应边相等可得EF=EF′,从而求出EF=BE-DE
∠BAD证明∠F′AE=∠FAE,然后利用“边角边"证明△F′AE和△FAE全等,根据全等三角形对应边相等可得EF=EF′,从而求出EF=BE-DE
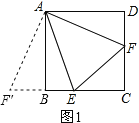
(1)如图1,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
∵∠EAF=45°,
∴∠EAF′=∠EAF=45°,
在△AEF和△AEF′中,
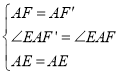
∴△AEF≌△AEF′(SAS),
∴EF=EF′
又EF′=BE+BF′=BE+DF
∴EF=BE+DF
(2)结论EF=BE+DF仍然成立.
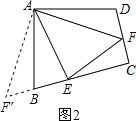
理由如下:如图2,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
则△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,∠ABF′=∠D,
又∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠EAF=∠DAF+∠BAE=∠BAE+∠BAF′,
∴∠EAF=∠EAF′,
又∵∠ABC+∠D=180°,
∴∠ABF′+∠ABE=180°,
∴F′、B、E三点共线,
在△AEF与△AEF′中,
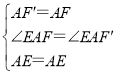
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′,
∴EF=BE+DF;
(3)发生变化.EF、BE、DF之间的关系是EF=BE-DF.
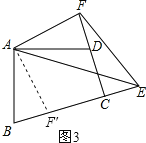
理由如下:如图3,将△ADF绕点A顺时针旋转,使AD与AB重合,点F落在BC上点F′处,得到△ABF′,
∴△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,
又∵∠EAF=![]() ∠BAD,且∠BAF′=∠DAF,
∠BAD,且∠BAF′=∠DAF,
∴∠F′AE=∠BAD-(∠BAF′+∠EAD)=∠BAD-(∠DAF+∠EAD)=∠BAD-∠FAE=∠FAE,
即∠F′AE=∠FAE,
在△F′AE与△FAE中,
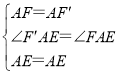
∴△F′AE≌△FAE(SAS),
∴EF=EF′,
又∵BE=BF′+EF′,
∴EF′=BE-BF′,
即EF=BE-DF.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案