ÌâÄ¿ÄÚÈÝ
 £¨2013•ÇàÑòÇøһģ£©Èçͼ£¬Å×ÎïÏßy=ax2+bx+cÓëxÖáÓÐÁ½¸ö²»Í¬µÄ½»µãA£¨x1£¬0£©¡¢B£¨x2£¬0£©£¨x1£¼x2£©£¬ÓëyÖáµÄÕý°ëÖá½»ÓÚµãC£¨0£¬3£©£®ÒÑÖª¸ÃÅ×ÎïÏߵĶ¥µãºá×ø±êΪ1£¬A¡¢BÁ½µã¼äµÄ¾àÀëΪ4£®
£¨2013•ÇàÑòÇøһģ£©Èçͼ£¬Å×ÎïÏßy=ax2+bx+cÓëxÖáÓÐÁ½¸ö²»Í¬µÄ½»µãA£¨x1£¬0£©¡¢B£¨x2£¬0£©£¨x1£¼x2£©£¬ÓëyÖáµÄÕý°ëÖá½»ÓÚµãC£¨0£¬3£©£®ÒÑÖª¸ÃÅ×ÎïÏߵĶ¥µãºá×ø±êΪ1£¬A¡¢BÁ½µã¼äµÄ¾àÀëΪ4£®£¨1£©ÇóÕâÌõÅ×ÎïÏߵĽâÎöʽ£»
£¨2£©Çó¡÷ABCÍâ½ÓÔ²µÄÔ²ÐÄMµÄ×Ý×ø±ê£»
£¨3£©ÔÚÅ×ÎïÏßÉÏÊÇ·ñ´æÔÚÒ»µãP£¬Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2Á½²¿·Ö£¿Èô´æÔÚ£¬ÇëÇó³öµãPµÄ×ø±ê£»Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
·ÖÎö£º£¨1£©ÒòΪÅ×ÎïÏßy=ax2+bx+cÓëxÖáÓÐÁ½¸ö²»Í¬µÄ½»µãA£¨x1£¬0£©£¬B£¨x2£¬0£©£¨x1£¼x2£©£¬ËùÒÔAºÍB¹ØÓÚÅ×ÎïÏߵĶԳÆÖá¶Ô³Æ£¬ÓÚÊÇ
=1¢Ù£»ÓÖÒòΪA¡¢BÁ½µã¼äµÄ¾àÀëΪ4£¬ÇÒx1£¼x2£¬ËùÒÔx2-x1=4¢Ú£¬½«¢Ù¢Ú×é³É·½³Ì×飬½â³öx1£¬x2µÄÖµ£¬ÔÙ½«µãA¡¢B¡¢CµÄ×ø±ê´úÈëy=ax2+bx+c£¬ÔËÓôý¶¨ÏµÊý·¨¼´¿ÉÇó³öÅ×ÎïÏߵĽâÎöʽ£»
£¨2£©¸ù¾ÝÈý½ÇÐÎÍâÐĵĶ¨Òå¿ÉÖªMA=MB=MC£¬ÓÉMA=MB¼°A¡¢BÁ½µãµÄ×ø±ê£¬µÃ³öÔ²ÐÄMµÄºá×ø±êΪ1£¬ÉèM£¨1£¬y£©£¬¸ù¾ÝMA=MCÁгö·½³Ì£¬¼´¿ÉÇó³öMµÄ×Ý×ø±ê£»
£¨3£©ÉèPDÓëBMµÄ½»µãΪE£¬·Ö³ÉÁ½ÖÖÇé¿ö¿¼ÂÇ£º¢Ùµ±¡÷BPEµÄÃæ»ýÊÇ¡÷BDEµÄ2±¶Ê±£¬ÓÉÓÚ¡÷BDEºÍ¡÷BPDͬ¸ß²»µÈµ×£¬ÄÇôËüÃǵÄÃæ»ý±ÈµÈÓڵױߵıȣ¬¼´DE=
PD£¬¿ÉÉè³öPµãµÄ×ø±ê£¬ÄÇôEµãµÄ×Ý×ø±êÊÇPµã×Ý×ø±êµÄ
£¬BDµÄ³¤ÎªB¡¢Pºá×ø±ê²îµÄ¾ø¶ÔÖµ£¬ÓÉÓÚ¡ÏOBC=45¡ã£¬ÄÇôBD=DE£¬¿ÉÒÔ´Ë×÷ΪµÈÁ¿¹ØϵÇó³öPµãµÄ×ø±ê£»¢Úµ±¡÷BDEµÄÃæ»ýÊÇ¡÷BPEµÄ2±¶Ê±£¬·½·¨Í¬¢Ù£®
| x1+x2 |
| 2 |
£¨2£©¸ù¾ÝÈý½ÇÐÎÍâÐĵĶ¨Òå¿ÉÖªMA=MB=MC£¬ÓÉMA=MB¼°A¡¢BÁ½µãµÄ×ø±ê£¬µÃ³öÔ²ÐÄMµÄºá×ø±êΪ1£¬ÉèM£¨1£¬y£©£¬¸ù¾ÝMA=MCÁгö·½³Ì£¬¼´¿ÉÇó³öMµÄ×Ý×ø±ê£»
£¨3£©ÉèPDÓëBMµÄ½»µãΪE£¬·Ö³ÉÁ½ÖÖÇé¿ö¿¼ÂÇ£º¢Ùµ±¡÷BPEµÄÃæ»ýÊÇ¡÷BDEµÄ2±¶Ê±£¬ÓÉÓÚ¡÷BDEºÍ¡÷BPDͬ¸ß²»µÈµ×£¬ÄÇôËüÃǵÄÃæ»ý±ÈµÈÓڵױߵıȣ¬¼´DE=
| 1 |
| 3 |
| 1 |
| 3 |
½â´ð£º½â£º£¨1£©¡ßÅ×ÎïÏßy=ax2+bx+cÓëxÖáÓÐÁ½¸ö²»Í¬µÄ½»µãA£¨x1£¬0£©¡¢B£¨x2£¬0£©£¨x1£¼x2£©£¬ÇÒÅ×ÎïÏ߶¥µãµÄºá×ø±êΪ1£¬
¡à
=1£¬¼´x1+x2=2¢Ù£»
ÓÖ¡ßA¡¢BÁ½µã¼äµÄ¾àÀëΪ4£¬ÇÒx1£¼x2£¬
¡àx2-x1=4¢Ú£¬
¢ÙÓë¢Ú×é³É·½³Ì×é
£¬
½âµÃ
£¬
¡àA£¨-1£¬0£©£¬B£¨3£¬0£©£®
°ÑA£¨-1£¬0£©£¬B£¨3£¬0£©£¬C£¨0£¬3£©´úÈëy=ax2+bx+c£¬
µÃ
£¬
½âµÃ
£¬
¡àº¯Êý½âÎöʽΪy=-x2+2x+3£»
£¨2£©¡ß¡÷ABCÍâ½ÓÔ²µÄÔ²ÐÄÊÇM£¬
¡àMA=MB=MC£¬MµãÔÚÏ߶ÎABµÄ´¹Ö±Æ½·ÖÏßÉÏ£¬
¡ßA£¨-1£¬0£©£¬B£¨3£¬0£©£¬
¡àMµÄºá×ø±êΪ£º
=1£®
ÉèM£¨1£¬y£©£¬ÓÉMA=MC£¬
µÃ£¨1+1£©2+y2=12+£¨y-3£©2£¬
½âµÃy=1£®
¹Ê¡÷ABCÍâ½ÓÔ²µÄÔ²ÐÄMµÄ×Ý×ø±êΪ1£»
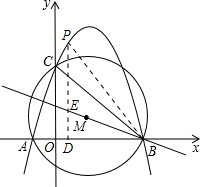 £¨3£©ÔÚÅ×ÎïÏßÉÏ´æÔÚÒ»µãP£¬Äܹ»Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2µÄÁ½²¿·Ö£®ÀíÓÉÈçÏ£º
£¨3£©ÔÚÅ×ÎïÏßÉÏ´æÔÚÒ»µãP£¬Äܹ»Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2µÄÁ½²¿·Ö£®ÀíÓÉÈçÏ£º
ÉèPDÓëBMµÄ½»µãΪE£¬¿ÉÇóÖ±ÏßBM½âÎöʽΪy=-
x+
£¬
ÉèP£¨x£¬-x2+2x+3£©£¬·ÖÁ½ÖÖÇé¿ö£º
¢Ùµ±S¡÷BED£ºS¡÷BEP=1£º2ʱ£¬PD=3DE£¬Èçͼ£®
Ôò-x2+2x+3=3£¨-
x+
£©£¬
ÕûÀí£¬µÃ2x2-7x+3=0£¬
½âµÃx=
»ò3£¬
¡à
»ò
£¨ÉáÈ¥£©£¬
¡àP£¨
£¬
£©£»
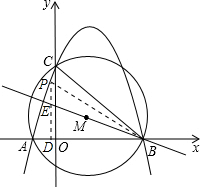 ¢Úµ±S¡÷PBE£ºS¡÷BED=1£º2ʱ£¬2PD=3DE£¬Èçͼ£®
¢Úµ±S¡÷PBE£ºS¡÷BED=1£º2ʱ£¬2PD=3DE£¬Èçͼ£®
Ôò2£¨-x2+2x+3£©=3£¨-
x+
£©£¬
ÕûÀí£¬µÃ4x2-11x-3=0£¬
½âµÃx=-
»ò3£¬
¡à
»ò
£¨ÉáÈ¥£©£¬
¡àP£¨-
£¬
£©£®
¹ÊÔÚÅ×ÎïÏßÉÏ´æÔÚµãP£¨
£¬
£©»òP£¨-
£¬
£©£¬Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2µÄÁ½²¿·Ö£®
¡à
| x1+x2 |
| 2 |
ÓÖ¡ßA¡¢BÁ½µã¼äµÄ¾àÀëΪ4£¬ÇÒx1£¼x2£¬
¡àx2-x1=4¢Ú£¬
¢ÙÓë¢Ú×é³É·½³Ì×é
|
½âµÃ
|
¡àA£¨-1£¬0£©£¬B£¨3£¬0£©£®
°ÑA£¨-1£¬0£©£¬B£¨3£¬0£©£¬C£¨0£¬3£©´úÈëy=ax2+bx+c£¬
µÃ
|
½âµÃ
|
¡àº¯Êý½âÎöʽΪy=-x2+2x+3£»
£¨2£©¡ß¡÷ABCÍâ½ÓÔ²µÄÔ²ÐÄÊÇM£¬
¡àMA=MB=MC£¬MµãÔÚÏ߶ÎABµÄ´¹Ö±Æ½·ÖÏßÉÏ£¬
¡ßA£¨-1£¬0£©£¬B£¨3£¬0£©£¬
¡àMµÄºá×ø±êΪ£º
| -1+3 |
| 2 |
ÉèM£¨1£¬y£©£¬ÓÉMA=MC£¬
µÃ£¨1+1£©2+y2=12+£¨y-3£©2£¬
½âµÃy=1£®
¹Ê¡÷ABCÍâ½ÓÔ²µÄÔ²ÐÄMµÄ×Ý×ø±êΪ1£»
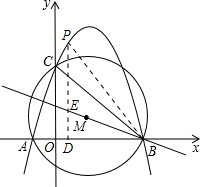 £¨3£©ÔÚÅ×ÎïÏßÉÏ´æÔÚÒ»µãP£¬Äܹ»Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2µÄÁ½²¿·Ö£®ÀíÓÉÈçÏ£º
£¨3£©ÔÚÅ×ÎïÏßÉÏ´æÔÚÒ»µãP£¬Äܹ»Ê¹¡÷PBD£¨PD´¹Ö±ÓÚxÖᣬ´¹×ãΪD£©±»Ö±ÏßBM·Ö³ÉÃæ»ý±ÈΪ1£º2µÄÁ½²¿·Ö£®ÀíÓÉÈçÏ£ºÉèPDÓëBMµÄ½»µãΪE£¬¿ÉÇóÖ±ÏßBM½âÎöʽΪy=-
| 1 |
| 2 |
| 3 |
| 2 |
ÉèP£¨x£¬-x2+2x+3£©£¬·ÖÁ½ÖÖÇé¿ö£º
¢Ùµ±S¡÷BED£ºS¡÷BEP=1£º2ʱ£¬PD=3DE£¬Èçͼ£®
Ôò-x2+2x+3=3£¨-
| 1 |
| 2 |
| 3 |
| 2 |
ÕûÀí£¬µÃ2x2-7x+3=0£¬
½âµÃx=
| 1 |
| 2 |
¡à
|
|
¡àP£¨
| 1 |
| 2 |
| 15 |
| 4 |
 ¢Úµ±S¡÷PBE£ºS¡÷BED=1£º2ʱ£¬2PD=3DE£¬Èçͼ£®
¢Úµ±S¡÷PBE£ºS¡÷BED=1£º2ʱ£¬2PD=3DE£¬Èçͼ£®Ôò2£¨-x2+2x+3£©=3£¨-
| 1 |
| 2 |
| 3 |
| 2 |
ÕûÀí£¬µÃ4x2-11x-3=0£¬
½âµÃx=-
| 1 |
| 4 |
¡à
|
|
¡àP£¨-
| 1 |
| 4 |
| 39 |
| 16 |
¹ÊÔÚÅ×ÎïÏßÉÏ´æÔÚµãP£¨
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 4 |
| 39 |
| 16 |
µãÆÀ£º´ËÌâÊǶþ´Îº¯ÊýµÄ×ÛºÏÀàÌâÄ¿£¬ÆäÖÐÉæ¼°µ½ÔËÓôý¶¨ÏµÊý·¨Çóº¯ÊýµÄ½âÎöʽ£¬¶þ´Îº¯ÊýµÄÐÔÖÊ£¬Èý½ÇÐεÄÍâÐÄ£¬Á½µã¼äµÄ¾àÀ빫ʽÒÔ¼°Í¼ÐÎÃæ»ýµÄÇ󷨵È֪ʶ£¬×ÛºÏÐÔÇ¿£¬ÄѶÈÉԴ󣬣¨3£©ÖнøÐзÖÀàÌÖÂÛÊǽâÌâµÄ¹Ø¼ü£®

Á·Ï°²áϵÁдð°¸
 ÔĶÁ¿ì³µÏµÁдð°¸
ÔĶÁ¿ì³µÏµÁдð°¸
Ïà¹ØÌâÄ¿
