题目内容
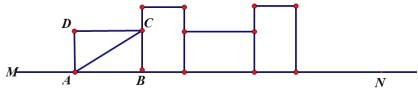
【题目】如图，在矩形ABCD中有对角线AC与BD相等，已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转至图②位置……依次类推，则:
(1)AC=__________.
(2)这样连续旋转2019次后，顶点B在整个旋转过程中所经过的路程之和是________.
【答案】5 3028π
【解析】
首先求得每一次转动的路线的长，发现每4次循环，找到规律然后计算即可．
（1）∵AB2+BC2=AC2, AB=4,BC=3,
∴AC2= 42+32=25,
∴AC=5；
（2）转动一次B的路线长是：0，转动第二次的路线长是：
π，转动第三次的路线长是：
π，转动第四次的路线长是：
=2π，以此类推，每四次循环，
2019÷4=504余3，
顶点B转动四次经过的路线长为：0+
+
+ 2π=6π,
连续旋转2019次经过的路线长为：6π×504+0++=3028π．
故答案为：（1）5；（2）3028π．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
