题目内容
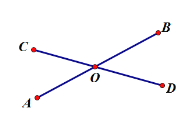
【题目】如图,已知O是直线AB上一点,∠AOC=45°36’,OD平分∠BOC,求∠AOD的度数.完成下列推理过程:
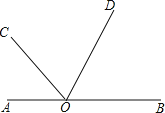
解:由题意可知,∠AOB是平角,
∠AOB= +∠BOC
因为∠AOC=45°36′
所以∠BOC= ° ′
又因为OD平分∠BOC
∴∠COD=![]() ∠BOC= ° ′
∠BOC= ° ′
∴∠AOD=∠ +∠ = ° ′
【答案】∠AOC,134,24,67,12,AOC,COD,112,48
【解析】
由平角定义得出∠AOB=∠AOC+∠BOC,求出∠BOC=134°24′,由角平分线定义的∠COD=![]() ∠BOC=67°12′,即可得出答案.
∠BOC=67°12′,即可得出答案.
由题意可知,∠AOB是平角,
则∠AOB=∠AOC+∠BOC,
因为∠AOC=45°36′,
所以∠BOC=134°24′,
又因为OD平分∠BOC,
∴∠COD=![]() ∠BOC=67°12′,
∠BOC=67°12′,
∴∠AOD=∠AOC+∠COD=112°48′;
故答案为:∠AOC,134,24,67,12,AOC,COD,112,48.

练习册系列答案
相关题目
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
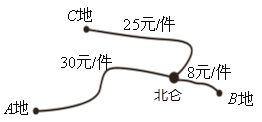
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.