题目内容
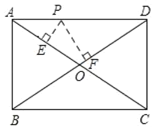
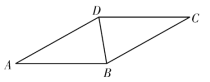
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.

(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=2![]() .
.
【解析】
(1)易得∠BAD=90°,∠AED=90°,根据余角的性质得∠BAE=∠ADE,结合等腰三角形的性质和圆周角定理,即可得到结论;
(2)由正切函数的定义得AB=![]() AD, AG=
AD, AG=![]() AB,从而得AG=2AD,即点D为AG的中点,进而得DH∥AF,结合∠AED=90°,即可得到结论;
AB,从而得AG=2AD,即点D为AG的中点,进而得DH∥AF,结合∠AED=90°,即可得到结论;
(3)根据正切三角函数的定义和勾股定理得AB=6,BD=3![]() ,结合三角形的面积公式,即可得到答案.
,结合三角形的面积公式,即可得到答案.
(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠BAE+∠DAE=90°,
∵AE⊥BD,
∴∠AED=90°,
∴∠DAE+∠ADE=90°,
∴∠BAE=∠ADE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ACB=∠ADE,
∴∠ABC=∠ADE=∠BAE,
∴FA=FB;
(2)由(1)知,∠ABC=∠ACB=∠ADB,
∵tan∠ACB=![]() ,
,
∴tan∠ABC=tan∠ADB=![]() ,
,
又∵∠BAD=90°,
∴在Rt△BAD中,AB=![]() AD,在Rt△BAG中,AG=
AD,在Rt△BAG中,AG=![]() AB,
AB,
∴AG=![]() (
(![]() AD)=2AD,
AD)=2AD,
∴点D为AG的中点,
又∵点H为FG的中点,
∴DH∥AF,
由(1)知,∠AED=90°,
∴∠HDE=∠AED=90°,
∴DH⊥OD,
∴DH为⊙O的切线;
(3)∵AD=3![]() ,
,
∴AB=![]() AD=6,
AD=6,
∴在Rt△ABD中,BD=![]() =3
=3![]() ,
,
∵S△ABD=![]() ABAD=
ABAD=![]() BDAE,
BDAE,
∴6×3![]() =3
=3![]() ×AE,
×AE,
∴AE=2![]() .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案