题目内容
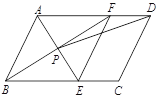
【题目】如图,在平行四边形ABCD中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]()
【解析】(1)先根据平行四边形性质以及角平分线性质,可得:AF//BE,∠AEB=∠BAE,∠AFB=∠ABF.根据等腰三角形性质可得:AB=BE,AF=AB.根据“一组对边平行且相等的四边形是平行四边形”证得四边形ABEF是平行四边形,再根据“一组邻边相等的平行四边形是菱形”证得平行四边形ABEF是菱形.
(2)作PH⊥AD于H.根据角的正切值的定义得tan∠ADP=![]() .根据菱形的性质,利用特殊角的三角函数,求得AH、PH长度,再根据HD=ADAH,即可得出tan∠ADP的值.
.根据菱形的性质,利用特殊角的三角函数,求得AH、PH长度,再根据HD=ADAH,即可得出tan∠ADP的值.
证明:(1)∵AE平分∠BAD BF平分∠ABC
∴∠BAE=∠EAF ∠ABF=∠EBF
∵AD//BC
∴∠EAF=∠AEB ∠AFB=∠EBF
∴∠BAE=∠AEB ∠AFB=∠ABF
∴AB=BE AB=AF
∴AF=AB=BE
∵AD//BC
∴ABEF为平行四边形
又AB=BE
∴ABEF为菱形
(2)如图所示,作PH⊥AD于H.
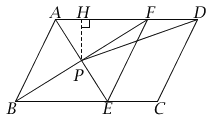
∵四边形ABEF是菱形,且∠ABC=60°,
∴△ABE为等边三角形,
∴∠FAE=60°,AE=AB=4,
则AP=![]() AE=2
AE=2
在Rt△APH中,由三角函数得:
PH=APsin60°=3![]() ,
,
AH=APcos60°=1,
∴HD=ADAH=5,
因此tan∠ADP=![]() =
=![]()

练习册系列答案
相关题目