题目内容
【题目】在△ABC中,![]() ,设c为最长边.当
,设c为最长边.当![]() 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长分别为6,8,11时,△ABC为______三角形.
(2)小明同学根据上述探究,有下面的猜想:“当![]() 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当![]() 时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
当![]() ,
,![]() 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
【答案】(1)锐角,钝角;(2)当4≤c<![]() 时,这个三角形是锐角三角形;当c=
时,这个三角形是锐角三角形;当c=![]() 时,这个三角形是直角三角形;当
时,这个三角形是直角三角形;当![]() <c<6时,这个三角形是钝角三角形.
<c<6时,这个三角形是钝角三角形.
【解析】(1)利用勾股定理列式求出两直角边为6、8时的斜边的值,然后作出判断即可;
(2)根据三角形的任意两边之和大于第三边求出最长边c点的最大值,然后得到c的取值范围,然后分情况讨论即可得解.
解:
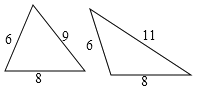
(1)∵两直角边分别为6、8时,斜边=![]() =10,
=10,
∴△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形;
故答案为:锐角;钝角;
(2)∵c为最长边,2+4=6,
∴4c<6,
a2+b2=22+42=20,
①a2+b2>c2,即c2<20, 4≤c<![]() ,
,
∴当4c<![]() 时,这个三角形是锐角三角形;
时,这个三角形是锐角三角形;
②a2+b2=c2,即c2=20,c=![]() ,
,
∴当c=![]() 时,这个三角形是直角三角形;
时,这个三角形是直角三角形;
③a2+b2<c2,即c2>20,c>![]() ,
,
∴当![]() <c<6时,这个三角形是钝角三角形.
<c<6时,这个三角形是钝角三角形.

 阅读快车系列答案
阅读快车系列答案【题目】(本题10分)某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?