题目内容
【题目】在直角坐标系中，O 为坐标原点，设点 P（1，m）在函数
的图象上，以 OP 为边作正方形OPQR，若反比例函数 
经过点 Q，则 k=______________．
【答案】2,-2
【解析】∵点P（1，m）在函数
的图象上，
∴m=
，
∴P（1， 
），
∴OP=
=2，
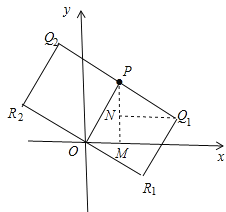
如图，作PM⊥x轴于M，QN⊥PM于N，
∵OM=1，PM=
，
∴tan∠POM=
=
，
∴∠POM=60°，
∴∠OPM=30°
∴∠QPN=90°-30°=60°，
∴∠POM=∠QPN，
在△POM和△QPN中，
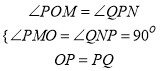
∴△POM≌△QPN，
∴PN=OM=1，NQ=PM=
，
∴Q1（1+
， 
-1），
同理证得Q2（1-
，1+
），
∴k=（1+
）×（
-1）=2，或k=（1+
）（1-
）=-2，
故答案为2或-2．
练习册系列答案
习题精选系列答案
相关题目
【题目】（本题10分）某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：
A | B | |
进价（万元/套） | 1.5 | 1.2 |
售价（万元/套） | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。
（毛利润=（售价 - 进价）×销售量）
（1）该商场计划购进A，B两种品牌的教学设备各多少套？
（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？
