��Ŀ����
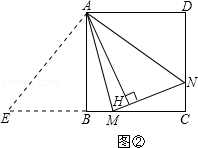
��֪��������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N��AH��MN�ڵ�H��
��1����ͼ�٣�����MAN��A��ת��BM=DNʱ������ֱ��д��AH��AB��������ϵ�� ��

��2����ͼ�ڣ�����MAN�Ƶ�A��ת��BM��DNʱ����1���з��ֵ�AH��AB��������ϵ�������������������д�����ɣ����������֤����

��3����ͼ�ۣ���֪��MAN=45�㣬AH��MN�ڵ�H����MH=2��NH=3����AH�ij����������ã�2���õ��Ľ��ۣ�

��1����ͼ�٣�����MAN��A��ת��BM=DNʱ������ֱ��д��AH��AB��������ϵ�� ��

��2����ͼ�ڣ�����MAN�Ƶ�A��ת��BM��DNʱ����1���з��ֵ�AH��AB��������ϵ�������������������д�����ɣ����������֤����

��3����ͼ�ۣ���֪��MAN=45�㣬AH��MN�ڵ�H����MH=2��NH=3����AH�ij����������ã�2���õ��Ľ��ۣ�

��1��AH=AB����2��������ϵ������֤���������������3��6��
�����������1����������ȫ�ȿ���֤��AH=AB��
��2���ӳ�CB��E��ʹBE=DN��֤����AEM�ա�ANM���ܵõ�AH=AB��
��3���ֱ���AM��AN���ۡ�AMH�͡�ANH���õ���ABM�͡�AND��Ȼ��ֱ��ӳ�BM��DN���ڵ�C����������ABCE����AH=x����MC=x��2��NC=x��3����Rt��MCN�У��ɹ��ɶ��������x��
�����������1����ͼ��AH=AB��
��2��������ϵ��������ͼ�ڣ��ӳ�CB��E��ʹBE=DN��
��ABCD�������Σ���AB=AD����D=��ABE=90�㣬��Rt��AEB��Rt��AND�У�
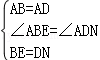 ����Rt��AEB��Rt��AND����AE=AN����EAB=��NAD�����EAM=��NAM=45�㣬�ڡ�AEM�͡�ANM�У�
����Rt��AEB��Rt��AND����AE=AN����EAB=��NAD�����EAM=��NAM=45�㣬�ڡ�AEM�͡�ANM�У�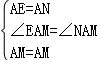 �����AEM�ա�ANM����AB��AH�ǡ�AEM�͡�ANM��Ӧ���ϵĸߣ���AB=AH��
�����AEM�ա�ANM����AB��AH�ǡ�AEM�͡�ANM��Ӧ���ϵĸߣ���AB=AH����3����ͼ�۷ֱ���AM��AN���ۡ�AMH�͡�ANH���õ���ABM�͡�AND����BM=2��DN=3����B=��D=��BAD=90�㣮�ֱ��ӳ�BM��DN���ڵ�C����������ABCD���ɣ�2����֪��AH=AB=BC=CD=AD����AH=x����MC=x��2��NC=x��3����Rt��MCN�У��ɹ��ɶ�������MN2=MC2+NC2����
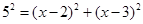 ��
�����
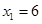 ��
��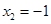 �����������⣬��ȥ������AH=6��
�����������⣬��ȥ������AH=6��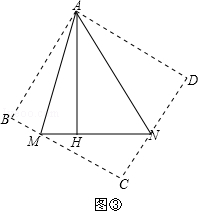

��ϰ��ϵ�д�
 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
�����Ŀ
 ��y�ᡢֱ��l�ֱ��ڵ�C��D�����ACD��y����תһ����Χ�ɼ�����ı������
��y�ᡢֱ��l�ֱ��ڵ�C��D�����ACD��y����תһ����Χ�ɼ�����ı������


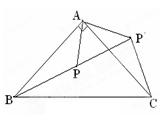
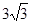
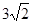
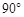 ���á�ABF������EF����EF�ij����� ��
���á�ABF������EF����EF�ij����� ��
 =�� ����
=�� ����