题目内容
【题目】某施工地在道路拓宽施工时，遇到这样一个问题，马路旁边原有一个面积为100平方米，周长为90米的三角形绿化地，由于马路拓宽绿地被占去了一部分△ADE，变成了四边形BCED且DE∥BC，原绿化地一边AB的长由原来的30米缩短成BD为18米．求被占去的部分面积有多大？它的周长是多少？
【答案】C△ADE＝36m， S△ADE＝16（m2）．
【解析】
首先证明△ADE∽△ABC，求出相似比，然后根据相似三角形的性质列出比例式求△ADE的周长和面积即可．
解：∵DE∥BC，
∴△ADE∽△ABC，
∴
，
∵AB的长由原来的30米缩短成BD为18米，
∴AD＝12m，
∴
，
解得：C△ADE＝36（m），
∵
，
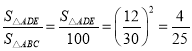∴S△ADE＝16（m2）．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
