题目内容
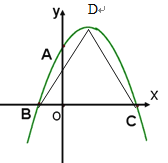
【题目】如图，二次函数
图象与
轴交于A、B与
轴交于C，OA=2，OB=1 ，OC=4
（1）.求二次函数解析式；
（2）.若点D为抛物线的顶点，求△BCD的面积.
【答案】（1）y=-
(x+1)(x-4)；（2）
【解析】
（1）先分别根据OA=2，OB=1 ，OC=4结合图象求得A,B,C的坐标，设交点式，将A点坐标代入即可求出函数解析式；
（2）根据B，C两点坐标可求得函数的对称轴，由此可求得函数的顶点坐标，根据三角形的面积公式计算面积即可.
解：(1)由题可知A(0,2),B(-1,0),C(4,0)
设函数解析式为y=a(x+1)(x-4)
代入A(0,2)得：2=a×1×（-4）
所以a=
所以函数解析式为：y=- (x+1)(x-4)
(2)(-1+4)÷2=
当x=时y=-×(+1) ×(-4)= 
所以顶点坐标为（，）
BC=OB+OC=1+4=5
所以S△BCD=×5×=
练习册系列答案
相关题目
