题目内容
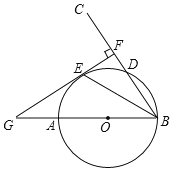
【题目】如图1,![]() 是
是![]() 内任意一点,连接
内任意一点,连接![]() ,分别以
,分别以![]() 为边作
为边作![]() (
(![]() 在
在![]() 的左侧)和
的左侧)和![]() (
(![]() 在
在![]() 的右侧),使得
的右侧),使得![]() ,
,![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
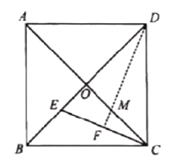
(2)如图2,![]() 交于点
交于点![]() ,若
,若![]() ,点
,点![]() 共线,其他条件不变,
共线,其他条件不变,
①判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②当![]() ,
,![]() ,且四边形
,且四边形![]() 是正方形时,直接写出
是正方形时,直接写出![]() 的长.
的长.

【答案】(1)证明见解析;(2)①四边形![]() 是矩形.理由见解析;②
是矩形.理由见解析;②![]() .
.
【解析】
(1)根据![]() ,得到
,得到![]() ,
,![]() ,再证
,再证![]() ,
,![]()
方法一:通过证明![]() ,
,![]() ,从而四边形
,从而四边形![]() 是平行四边形,
是平行四边形, ![]() ,所以为矩形.
,所以为矩形.
方法二:证明![]()
方法三:证![]() ,
,![]() ,
,![]() .
.
(1)∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,即.
,即.![]() .
.
∴![]() .
.
(2)①四边形![]() 是矩形.理由如下:
是矩形.理由如下:
方法一:由(1)知,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,即
,即![]() .
.
∴![]() . ∴
. ∴![]() .
.
∵![]() . ∴
. ∴![]() .
.
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
方法二:如图
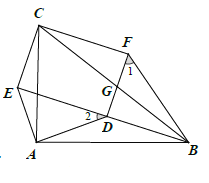
由(1)知![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,
,![]() ,即
,即![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,
共线,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是矩形.
是矩形.
方法三:由(1)知,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(1)知![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() . ∵
. ∵![]() ,∴
,∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
②![]()

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目