题目内容
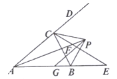
【题目】如图，在梯形ABCD中，AD∥BC
，点E是边AD的中点，连接BE交AC于F，BE的延长线交CD的延长线于G.
（1）求证：
；
（2）若GE=2，BF=3，求线段EF的长．
【答案】（1）见解析（2）1.
【解析】
（1）由于AD∥BC，易证得△GED∽△GBC；得GE：GB＝DE：BC；已知AE＝DE，代换相等线段后即可得出本题要证的结论；
（2）按照（1）的方法，可由AE∥BC，得出AE：BC＝EF：FB，再联立（1）得出的比例关系式，可列出关于EF的方程，即可求得EF的长.
解：（1）证明：
∵AD∥BC，
∠GED＝∠GBC，
∠G＝∠G，
∴△GED∽△GBC，
GE：GB=DE：BC，
∵AE＝DE，
∴EG：GB=AE：BC；
（2）∵AD∥BC，
∴△AEF∽△CBF，
AE：BC=EF：BF，
由(1)问EG：GB=AE：BC，
∴EG：GB=EF：BF，
设EF＝x，
∵GE＝2，BF＝3，
∴x：3=2：(5+x),
x1＝1，x2＝－6（不合题意，舍去）
∴EF＝1．
练习册系列答案
相关题目
