题目内容
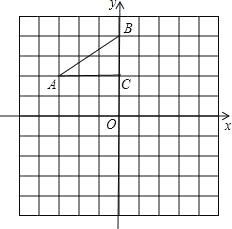
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
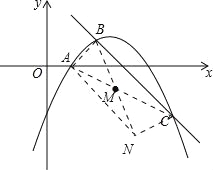
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
【解析】
试题分析:(1)根据当x=0和x=5时所对应的函数值相等,可得(5,c),根据待定系数法,可得函数解析式;
(2)联立抛物线与直线,可得方程组,根据解方程组,可得B、C点坐标,根据勾股定理,可得AB的长;
(3)根据线段中点的性质,可得M点的坐标,根据旋转的性质,可得MN与BM的关系,根据平行四边形的判定,可得答案.
试题解析:(1)当x=0时,y=c,即(0,c).
由当x=0和x=5时所对应的函数值相等,得(5,c).
将(5,c)(1,0)代入函数解析式,得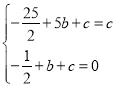 ,解得
,解得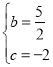 .
.
故抛物线的解析式为y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)联立抛物线与直线,得
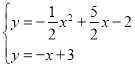 ,解得
,解得![]() ,
,![]() ,即B(2,1),C(5,﹣2).
,即B(2,1),C(5,﹣2).
由勾股定理,得AB=![]() =
=![]() ;
;
(3)如图:
 ,
,
四边形ABCN是平行四边形,∵M是AC的中点,∴AM=CM.
∵点B绕点M旋转180°得到点N,∴BM=MN,
∴四边形ABCN是平行四边形.

练习册系列答案
相关题目