题目内容
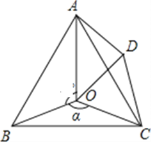
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=130°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
【答案】(1)见解析;(2) ![]() 是直角三角形,理由见解析;(3) 115°或100°或130°.
是直角三角形,理由见解析;(3) 115°或100°或130°.
【解析】
(1)根据![]() 得
得![]() ,则
,则![]() 是等腰三角形,又
是等腰三角形,又![]() ,故
,故![]() 是等边三角形;
是等边三角形;
(2)根据![]() 可得
可得![]() ,即
,即![]() ,由题(1)可得
,由题(1)可得![]() ,则
,则![]() ,故
,故![]() 是有一个锐角为
是有一个锐角为![]() 的直角三角形;
的直角三角形;
(3)由题(2)可知:![]() ,由三角形内角和定理得
,由三角形内角和定理得![]() ,然后分哪两个角为底角建立等式求解即可.
,然后分哪两个角为底角建立等式求解即可.
(1)![]()
![]()
![]() 是等腰三角形
是等腰三角形
又![]()
![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,
时,![]() 是直角三角形.理由如下:
是直角三角形.理由如下:
![]()
![]() ,即
,即![]()
由题(1)的结论可得![]()
![]()
![]() 是有一个锐角为
是有一个锐角为![]() 的直角三角形;
的直角三角形;
(3)由题(2)可知:![]()
则在![]() 中,
中,![]()
当![]() 时,
时,![]() 是等腰三角形,解得
是等腰三角形,解得![]()
当![]() 时,
时,![]() 是等腰三角形,解得
是等腰三角形,解得![]()
当![]() 时,
时,![]() 是等腰三角形,解得
是等腰三角形,解得![]()
综上,当![]() 为
为![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
相关题目







