题目内容
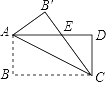
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,把△ABC沿对角线AC折叠,得到△AB'C,B'C与AD相交于点E,则AE的长________.
【答案】5cm
【解析】证出△AEC是等腰三角形:AE=CE,然后设AE=x,则CE=x,DE=6﹣x.在Rt△CDE中,由勾股定理得出方程,解方程即可.
∵四边形ABCD是矩形,∴AD∥BC,AD=BC=8cm,CD=AB=4cm,∴∠ACB=∠DAC.
由折叠的性质得:∠ACB=∠ECA,∴∠DAC=∠ECA,∴AE=CE.
设AE=x,则CE=x,DE=8﹣x.在Rt△CDE中,DE2+CD2=CE2.
即(8﹣x)2+42=x2,解得:x=5.
即AE=5.
故答案为:5cm.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目