题目内容
【题目】如图,在长方形ABCD中,AB=8 cm,AD=4 cm,将ΔABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点。
(1)证明:AF=CF;
(2)求ΔAFC的面积.
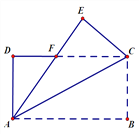
【答案】(1)见解析;(2)10平方厘米
【解析】试题分析:(1)根据长方形性质得出∠D=90°,AD=BC,AB=DC=8cm,根据折叠的性质得出∠D=∠E=90°,CE=BC=AD,根据全等三角形的判定得出即可;
(2)先证明△EFC≌△DFA,得出DF=EF,AF=CF,设FC=x,在RT△ADF中利用勾股定理可得出x的值,再根据三角形面积公式计算即可.
试题解析:
(1)∵四边形ABCD是长方形,
∴∠D=90°,AD=BC,AB=DC=8cm,
∵将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点,
∴∠D=∠E=90°,CE=BC=AD,
在△ADF和△CEF中
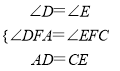 ,
,
∴△ADF≌△CEF(AAS),
∴AF=CF;
(2)∵△EFC≌△DFA(已证)
∴DF=EF,AF=CF,
设FC=x,则DF=8-x,
在RT△ADF中,DF2+AD2=AF2,即(8-x)2+16=x2,
解得:x=5,
即CF=5cm,
∴重叠部分△ACF的面积=![]() CFAD=
CFAD=![]() ×5×4=10cm2.
×5×4=10cm2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问 卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成 了不完整的表格和扇形统计图(如图).
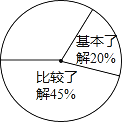
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为 人,表中m的值为 ;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?