题目内容
小晶和小红玩掷骰子游戏,每人将一个各面分别标有数字1、2、3、4、5、6的正方体骰子掷一次,把两人掷得的点数相加,并约定:若点数之和等于6,则小晶赢;若点数之和等于7,则小红赢;若点数之和是其他数,则两人不分胜负,那么( )
| A、小晶赢的机会大 | B、小红赢的机会大 | C、小晶、小红赢的机会一样大 | D、不能确定 |
分析:先通过列表得到共有36种等可能的结果,其中点数之和等于6的占5种,点数之和等于7的占6种,再根据概率的定义得到P(小晶赢)=
;P(小红赢)=
=
,即可得到答案.
| 5 |
| 36 |
| 6 |
| 36 |
| 1 |
| 6 |
解答: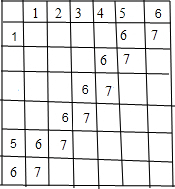 解:列表如下:
解:列表如下:
共有36种等可能的结果,其中点数之和等于6的占5种,点数之和等于7的占6种,
∴P(小晶赢)=
;P(小红赢)=
=
,
即P(小晶赢)<P(小红赢),
所以小红赢的机会大.
故选B.
 解:列表如下:
解:列表如下:共有36种等可能的结果,其中点数之和等于6的占5种,点数之和等于7的占6种,
∴P(小晶赢)=
| 5 |
| 36 |
| 6 |
| 36 |
| 1 |
| 6 |
即P(小晶赢)<P(小红赢),
所以小红赢的机会大.
故选B.
点评:本题考查了游戏公平性问题:先利用列表或树状图法展示所有等可能的结果数,然后找出两个事件所发生的结果数,根据概率的定义计算出它们的概率,然后通过概率的大小判断游戏是否公平.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目