题目内容
(2008•无锡)小晶和小红玩掷骰子游戏,每人将一个各面分别标有1,2,3,4,5,6的正方体骰子掷一次,把两人掷得的点数相加,并约定:点数之和等于6,小晶赢;点数之和等于7.小红赢;点数之和是其它数,两人不分胜负.问他们两人谁获胜的概率大?请你用“画树状图”或“列表”的方法加以分析说明.
【答案】分析:用列举法列举出符合题意的各种情况的个数,再根据概率公式解答,比较即可.
解答:解:画出树状图:
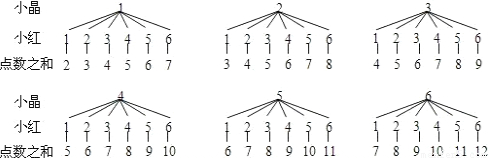
由表或图可知,点数之和共有36种可能的结果,其中6出现5次,7出现6次,
故P(和为6)=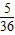 ,P(和为7)=
,P(和为7)=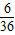 .
.
∵P(和为6)<P(和为7),
∴小红获胜的概率大.
评分说明:列表正确或画对树状图得(4分),两个概率每求对一个得(1分),比较后得出结论再得(1分).
点评:情景设置略加改编,使学生倍感亲切体现“课标”理念是本卷中的一大亮点.此题考查的是用列表法或者用树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
解答:解:画出树状图:

由表或图可知,点数之和共有36种可能的结果,其中6出现5次,7出现6次,
故P(和为6)=
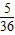 ,P(和为7)=
,P(和为7)=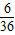 .
.∵P(和为6)<P(和为7),
∴小红获胜的概率大.
评分说明:列表正确或画对树状图得(4分),两个概率每求对一个得(1分),比较后得出结论再得(1分).
点评:情景设置略加改编,使学生倍感亲切体现“课标”理念是本卷中的一大亮点.此题考查的是用列表法或者用树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
(2008•无锡)小明所在学校初三学生综合素质评定分A,B,C,D四个等第,为了了解评定情况,小明随机调查了初三30名学生的学号及他们的评定等汲,结果整理如下:
注:等级A,B,C,D分别代表优秀、良好、合格、不合格.
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?

| 学号 | 3003 | 3008 | 3012 | 3016 | 3024 | 3028 | 3042 | 3048 | 3068 | 3075 |
| 等第 | A | C | B | C | D | B | A | B | B | A |
| 学号 | 3079 | 3088 | 3091 | 3104 | 3116 | 3118 | 3122 | 3136 | 3144 | 3154 |
| 等第 | B | B | B | C | A | C | B | A | A | B |
| 学号 | 3156 | 3163 | 3172 | 3188 | 3193 | 3199 | 3201 | 3208 | 3210 | 3229 |
| 等第 | C | A | B | B | A | B | C | C | B | B |
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?

(2008•无锡)小明所在学校初三学生综合素质评定分A,B,C,D四个等第,为了了解评定情况,小明随机调查了初三30名学生的学号及他们的评定等汲,结果整理如下:
注:等级A,B,C,D分别代表优秀、良好、合格、不合格.
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?

| 学号 | 3003 | 3008 | 3012 | 3016 | 3024 | 3028 | 3042 | 3048 | 3068 | 3075 |
| 等第 | A | C | B | C | D | B | A | B | B | A |
| 学号 | 3079 | 3088 | 3091 | 3104 | 3116 | 3118 | 3122 | 3136 | 3144 | 3154 |
| 等第 | B | B | B | C | A | C | B | A | A | B |
| 学号 | 3156 | 3163 | 3172 | 3188 | 3193 | 3199 | 3201 | 3208 | 3210 | 3229 |
| 等第 | C | A | B | B | A | B | C | C | B | B |
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?

(2008•无锡)小明所在学校初三学生综合素质评定分A,B,C,D四个等第,为了了解评定情况,小明随机调查了初三30名学生的学号及他们的评定等汲,结果整理如下:
注:等级A,B,C,D分别代表优秀、良好、合格、不合格.
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?

| 学号 | 3003 | 3008 | 3012 | 3016 | 3024 | 3028 | 3042 | 3048 | 3068 | 3075 |
| 等第 | A | C | B | C | D | B | A | B | B | A |
| 学号 | 3079 | 3088 | 3091 | 3104 | 3116 | 3118 | 3122 | 3136 | 3144 | 3154 |
| 等第 | B | B | B | C | A | C | B | A | A | B |
| 学号 | 3156 | 3163 | 3172 | 3188 | 3193 | 3199 | 3201 | 3208 | 3210 | 3229 |
| 等第 | C | A | B | B | A | B | C | C | B | B |
(1)请在下面给出的图中画出这30名学生综合素质评定等级的频数条形统计图,并计算其中等级达到良好以上(含良好)的频率;
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等级达到良好以上(含良好)的人数?
