题目内容
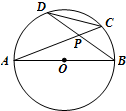 已知AB是⊙O的直径,弦AC与BD交于点P,若CD=5,AB=13,则cos∠APD等于
已知AB是⊙O的直径,弦AC与BD交于点P,若CD=5,AB=13,则cos∠APD等于
- A.
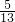
- B.
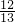
- C.
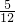
- D.
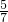
A
分析:连接AD.根据直径所对的圆周角是直角,得∠ADB=90°;根据两角对应相等,两三角形相似得△APB∽△DPC,则PD:PA=CD:AB=5:13;再根据锐角三角函数的定义求得cos∠APD的值.
解答: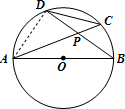 解:连接AD.
解:连接AD.
∵AB为⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角).
∵∠BAP=∠CDP(同弧所对的圆周角相等),∠APB=∠DPC(对顶角相等),
∴△APB∽△DPC,
∴PD:PA=CD:AB=5:13(相似三角形的对应边成比例),
∴cos∠APD=PD:PA=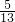 .
.
故选A.
点评:此题综合运用了圆周角定理的推论、相似三角形的判定和性质、以及锐角三角函数的概念.解答该题的关键是通过作辅助线AD构建直角三角形ABD,在直角三角形中利用锐角三角函数的定义求cos∠APD的值.
分析:连接AD.根据直径所对的圆周角是直角,得∠ADB=90°;根据两角对应相等,两三角形相似得△APB∽△DPC,则PD:PA=CD:AB=5:13;再根据锐角三角函数的定义求得cos∠APD的值.
解答:
 解:连接AD.
解:连接AD.∵AB为⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角).
∵∠BAP=∠CDP(同弧所对的圆周角相等),∠APB=∠DPC(对顶角相等),
∴△APB∽△DPC,
∴PD:PA=CD:AB=5:13(相似三角形的对应边成比例),
∴cos∠APD=PD:PA=
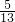 .
.故选A.
点评:此题综合运用了圆周角定理的推论、相似三角形的判定和性质、以及锐角三角函数的概念.解答该题的关键是通过作辅助线AD构建直角三角形ABD,在直角三角形中利用锐角三角函数的定义求cos∠APD的值.

练习册系列答案
相关题目
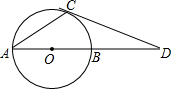 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=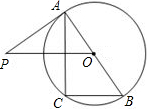 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,