题目内容
【题目】小明和小亮用如下的同一个转盘进行“配紫色”游戏．游戏规则如下：连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色）,则小明得1分,否则小亮得1分．你认为这个游戏对双方是否公平？请说明理由．
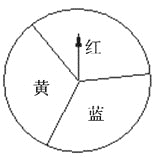
【答案】游戏不公平．
【解析】
试题游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等．
试题解析：
第二次 | 红 | 黄 | 蓝 |
红 | （红,红） | （红,黄） | （红,蓝） |
黄 | （黄,红） | （黄,黄） | （黄,蓝） |
蓝 | （蓝,红） | （蓝,黄） | （蓝,蓝） |
从表中可以得到：P（小明获胜）=
,P（小亮获胜）=
．
∴小明的得分为×1=,小亮的得分为×1=．
∵＞,
∴游戏不公平．
练习册系列答案
相关题目
【题目】甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
（1）计算出现向上点数为6的频率．
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请判断丙的说法是否正确并说明理由．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和为3的倍数的概率．
