题目内容
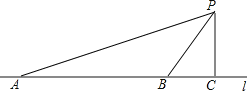
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() .
.
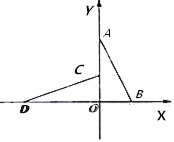
(1)求点![]() 的坐标;
的坐标;
(2)求证![]() ;
;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出点
为腰的等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)(0,5);(2)见解析;(3)(1,0)、(-25,0)或(12,0)
【解析】
(1)由![]() 求出
求出![]() ,证明△AOB≌△DOC,从而得到OC=OB=5,再写出点C的坐标即可;(2)由△AOB≌△DOC可得∠CDO=∠BAO,因为∠ABO+∠BAO=90°,则∠ABO+∠CDO=90°,从而得证;(3)分CD=DP或CD=CP两种情况求解即可.
,证明△AOB≌△DOC,从而得到OC=OB=5,再写出点C的坐标即可;(2)由△AOB≌△DOC可得∠CDO=∠BAO,因为∠ABO+∠BAO=90°,则∠ABO+∠CDO=90°,从而得证;(3)分CD=DP或CD=CP两种情况求解即可.
(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴△AOB≌△DOC,
∴OC=OB=5,
∴点![]() 的坐标为(0,5);
的坐标为(0,5);
(2)∵△AOB≌△DOC,
∴∠CDO=∠BAO,
∵∠ABO+∠BAO=90°,
∴∠ABO+∠CDO=90°,
∴![]() ;
;
(3)若CD=DP,则DP=DO+OP=12+OP=13,故OP=1,点P的坐标为(1,0);
或OP=DO+CD=12+13=25,点P在x轴的负半轴上,故点P的坐标为(-25,0);
若CD=CP,则DO=OP=12,点P的坐标为(12,0);
综上,点P的坐标为(1,0)、(-25,0)或(12,0).

 手拉手全优练考卷系列答案
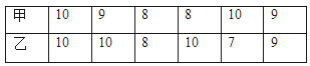
手拉手全优练考卷系列答案【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
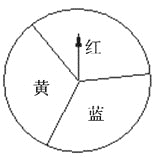
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |
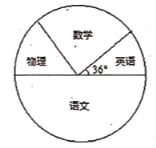
(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.