题目内容
【题目】如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）
A.nB.n﹣1C.
D.
n
【答案】B
【解析】
根据题意可得，阴影部分的面积是正方形的面积的
，已知两个正方形可得到一个阴影部分，则n个这样的正方形重叠部分即为（n-1）个阴影部分的和．
解：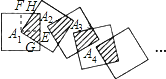
作A1E⊥A2E，A1F⊥A2H．
则∠FA1E=∠H A1G=90°，
∴∠FA1H=∠G A1E，
在△A1HF和△A1GE中，
∴△A1HF≌△A1GE，
∴四边形A2H A1G的面积=四边形A1E A2F的面积=×4=1，
同理，各个重合部分的面积都是1．则n个这样的正方形重叠部分（阴影部分）的面积和为
1×（n-1）=n-1
练习册系列答案
高效智能课时作业系列答案
相关题目
