题目内容
【题目】如图,正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 从
从![]() 点出发,以
点出发,以![]() 秒的速度沿折线
秒的速度沿折线![]() 匀速运动,到
匀速运动,到![]() 点停止运动,设
点停止运动,设![]()
![]() 的面积为
的面积为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒.
秒.

(1)点![]() 运动到点
运动到点![]() ,
,![]() = .点
= .点![]() 运动到点
运动到点![]() ,
,![]() = .
= .
(2)请你用含![]() 的式子表示y.
的式子表示y.
【答案】(1)1;3;(2)y=t+1(0≤t<1)和y=2(1≤t≤3).
【解析】
(1)由题意直接根据时间等于路程除以速度进行分析即可求得;
(2)根据题意分成两种情况进行分析,利用三角形面积公式即可得解.
解:(1)∵正方形ABCD中,AB=2cm,
∴CD=AB=BC=AD=2cm,
∵M是CD的中点,
∴MC=1cm,
∵点P从M点出发,以1cm/秒的速度沿折线MC-CB匀速运动,
∴点P运动到点C,t=1,点P运动到点B,t=3,
故答案为1;3;
(2)设△ADP的面积为ycm2,点P运动时间为t秒,
当P在MC上时,y=![]() ADDP=
ADDP=![]() ×2×(1+t)=t+1(0≤t<1);
×2×(1+t)=t+1(0≤t<1);
当P在BC上时,y=![]() ADDC=
ADDC=![]() ×2×2=2(1≤t≤3).
×2×2=2(1≤t≤3).
综上所述可得:y=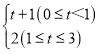 .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?