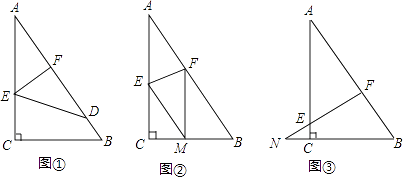题目内容
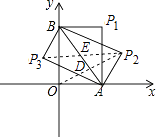
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 . 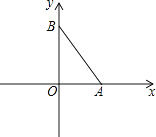
【答案】(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )
)
【解析】解:如图所示:
①∵OA=3,OB=4,
∴P1(3,4);
②连结OP2 ,
设AB的解析式为y=kx+b,则![]() ,
,
解得 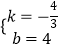 .
.
故AB的解析式为y=﹣ ![]() x+4,
x+4,
则OP2的解析式为y= ![]() x,
x,
联立方程组得 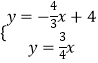 ,
,
解得 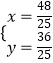 ,
,
则P2( ![]() ,
, ![]() );
);
③连结P2P3 ,
∵(3+0)÷2=1.5,
(0+4)÷2=2,
∴E(1.5,2),
∵1.5×2﹣ ![]() =﹣
=﹣ ![]() ,
,
2×2﹣ ![]() =
= ![]() ,
,
∴P3(﹣ ![]() ,
, ![]() ).
).
故点P的坐标为(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
故答案为:(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
本题考查了全等三角形的性质及坐标与图形的性质,做这种题要求对全等三角形的判定方法熟练掌握.由条件可知AB为两三角形的公共边,且△AOB为直角三角形,当△AOB和△APB全等时,则可知△APB为直角三角形,再分三种情况进行讨论,可得出P点的坐标.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=  且其日销售量y(kg)与时间t(天)的关系如表:
且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.