Question

【题目】如图，将矩形纸片ABCD裁剪出扇形ABE和⊙O，其中⊙O与 ，BC，CD都相切．若扇形ABE与⊙O恰好制作成一个圆锥，已知AB=8cm，则AD的长为 ．

Answer 1

【答案】10
【解析】解：∵AB=8，∠A=90°， ∴ = =4π，
∴⊙O的半径为2，
设⊙O与BC、CD分别相切于F、H，
连接FO并延长交AD于G，则FG垂直于AD，OH垂直于CD，连接OA．
可得矩形ABFG、矩形CDGF、矩形OHDG和正方形OFCH，
∴FE⊥BC，
∴OE=8﹣2=6，OA=8+2=10，
在Rt△AOG中，AG= =8，
∴AE=8=AG，
∴点E与G重合，
又DE=CF=2，
∴AD=AE+DE=10，
所以答案是10．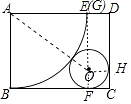

【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．