Question

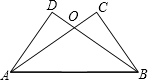
已知：如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．

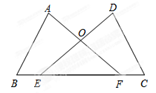
(1)求证：AB＝DC.(2)试判断△OEF的形状，并说明理由．

Answer 1

(1)见解析。(2)等腰三角形。理由哦见解析

试题分析：（1）求证AB=DC，可由AB、DC所在的两个三角形全等求得.由BE＝CF，可得BF=CE,此时易用AAS证明△ABF≌△DCE，即可得AB=DC.
（2）由（1）△ABF≌△DCE易得∠OEF＝∠OFE，所以OE=OF.注意本题属于判断说理题，答题应先判断结论，后说明理由.
试题解析：
（1）证明：∵BE＝CF
∴BF=CE
∵在△ABF和△DCE中
∠A＝∠D
∠B＝∠C
BF=CE
∴△ABF≌△DCE（AAS）
∴AB＝DC
（2）解：△OEF是等腰三角形
∵△ABF≌△DCE
∴∠AFB＝∠DEC
∴OE=OF
∴△OEF是等腰三角形