题目内容
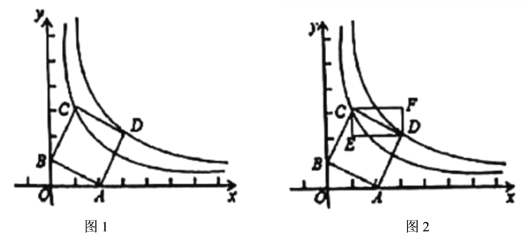
【题目】定义：如图（1），
，
，
，
四点分别在四边形
的四条边上，若四边形
为菱形，我们称菱形为四边形的内接菱形.
动手操作：
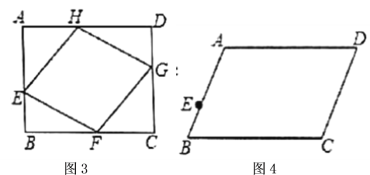
（1）如图2，网格中的每个小四边形都为正方形，每个小四边形的顶点叫做格点，由
个小正方形组成一个大正方形，点、在格点上，请在图（2）中画出四边形的内接菱形；
特例探索：
（2）如图3，矩形，
，点在线段
上且
，四边形是矩形的内接菱形，求
的长度；
拓展应用：
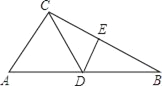
（3）如图4，平行四边形，，
，点在线段上且，
①请你在图4中画出平行四边形的内接菱形，点在边
上；
②在①的条件下，当
的长最短时，的长为__________
【答案】（1）详见解析；（2）3；（3）①详见解析；②
的长为
【解析】
（1）以EF为边，作一个菱形，使其各边长都为
；
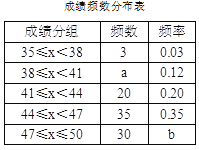
（2）如图2，连接HF，证明△DHG≌△BFE（AAS），可得CG＝3；
（3）①根据（2）中可知DG＝BE＝2，根据对角线垂直平分作内接菱形EFGH；
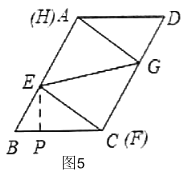
②如图5，当F与C重合，则A与H重合时，此时BF的长最小，就是BC的长，根据直角三角形30度角的性质和勾股定理计算可得结论．
（1）如图2所示，菱形
即为所求；
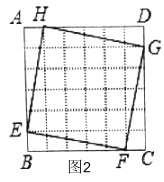
（2）如图3，连接
，
四边形
是矩形，
，
，
，
，
四边形是菱形，
，
，
，
，即
，
，
；
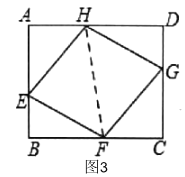
（3）①如图4所示，由（2）知：
，，
作法：作
，连接
，再作的垂直平分线，交
、于
、
，得四边形即为所求作的内接菱形；
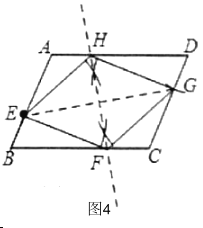
②如图5，当与
重合，则
与重合时，此时
的长最小，过
作
于
，
中，
，
，
，
，
四边形是菱形，
，
，
即当的长最短时，的长为
练习册系列答案
备战中考寒假系列答案
相关题目
