题目内容
【题目】抛物线m:y=x2﹣2x+2与直线l:y=x+2交于A,B(A在B的左侧),且抛物线顶点为C.
(1)求A,B,C坐标;
(2)若点D为该抛物线上的一个动点,且在直线AC下方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
(3)将抛物线m:y=x2﹣2x+2沿直线OC方向平移得抛物线m′,与直线l:y=x+2交于A′,B′,问在平移过程中线段A′B′的长度是否发生变化,请通过计算说明.
【答案】(1)A(0,2),B(3,5),C(1,1);(2)D(![]() ,
, ![]() );(3)A′B′的长度为定值,理由见解析
);(3)A′B′的长度为定值,理由见解析
【解析】试题分析:(1)利用配方法得到y=(x﹣1)2+1,从而可得到点C的坐标,然后将y=x2﹣2x+2与y=x+2可求得点A和点B的坐标;
(2)过点D作DE∥y轴,交抛物线与点P.先求得直线AC的解析式,设点D的坐标为(m,m2﹣2m+2),则点P的坐标为(m,﹣m+2),则PD=﹣m2+m,然后依据S△ACD=S△APD+S△CPD的到△ACD的面积与m的函数关系式,最后,利用配方法可求解即可.
(3)过点A′作A′M⊥x轴,垂足为M,B′N⊥x轴,垂足为N,作A′G⊥B′N,垂足为G,则A′B′=![]() A′G,设平移后抛物线的解析式为y=(x﹣a)2+a.A′(x1,y1)B′(x2,y2),依据完全平方公式得到A′G=
A′G,设平移后抛物线的解析式为y=(x﹣a)2+a.A′(x1,y1)B′(x2,y2),依据完全平方公式得到A′G=![]() .由将y=x+2代入y=(x﹣a)2+a得到关于x的方程,依据一元二次方程根与系数的关系可得到x2+x1=2a+1,x2x1=a2+a+2,从而可求得A′G的长,最后可得到A′B′的长.
.由将y=x+2代入y=(x﹣a)2+a得到关于x的方程,依据一元二次方程根与系数的关系可得到x2+x1=2a+1,x2x1=a2+a+2,从而可求得A′G的长,最后可得到A′B′的长.
试题解析:(1)∵y=x2﹣2x+2=(x﹣1)2+1,
∴C(1,1),
将y=x2﹣2x+2与y=x+2联立得: ![]() ,解得:
,解得: ![]() 或
或![]() ,
,
∴A(0,2),B(3,5);
(2)如图1所示:过点D作DE∥y轴,交抛物线与点P.
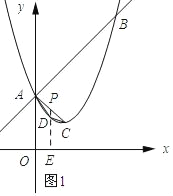
设AC的解析式为y=kx+b,将点A和点C的坐标代入得: ![]() ,解得k=﹣1,b=2,
,解得k=﹣1,b=2,
∴直线AC的解析式为y=﹣x+2,
设点D的坐标为(m,m2﹣2m+2),则点P的坐标为(m,﹣m+2),则PD=(﹣m+2)﹣(m2﹣2m+2)=﹣m2+m.
S△ACD=S△APD+S△CPD=![]() ×1DP=
×1DP=![]() (﹣m2+m)=﹣
(﹣m2+m)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,△ACD的面积有最大值,最大值为
时,△ACD的面积有最大值,最大值为![]() ,
,
此点D的坐标为(![]() ,
, ![]() );
);
(3)如图2所示:过点A′作A′M⊥x轴,垂足为M,B′N⊥x轴,垂足为N,作A′G⊥B′N,垂足为G,则A′B′=![]() A′G,
A′G,
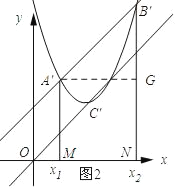
设OC的解析式为y=kx,将点C的坐标代入得到k=1,则OC的解析式为y=x,
设平移后抛物线的解析式为y=(x﹣a)2+a,
设A′(x1,y1)B′(x2,y2),则A′G=|x2﹣x1|=![]() ,
,
将y=x+2代入y=(x﹣a)2+a得:x2﹣(2a+1)x+a2+a+2=0,
∴x2+x1=2a+1,x2x1=a2+a+2.
∴A′G=![]() =3,
=3,
∴A′B′=3![]() ,
,
∴A′B′的长度为定值.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案