题目内容
【题目】如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3， 
)，点C的坐标为(
，0)，点P为斜边OB上的一个动点，则PA＋PC的最小值为( )
A. 
B. 
C. 
D. 2 
【答案】B
【解析】如图，作点A关于OB的对称点点D，连接CD交OB于点P，此时PA＋PC最小，作DN⊥x轴交于点N，
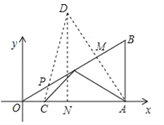
∵B（3， 
），∴OA=3，AB=
，∴OB=2
，∴∠BOA=30°，
∵在Rt△AMO中，∠MOA=30°，AO=3，∴AM=1.5，∠OAM=60°，∴∠ADN=30°，
∵在Rt△AND中，∠ADN=30°，AD=2AM=3，∴AN=1.5，DN=
，
∴CN=3－
－1.5=1，
∴CD2=CN2+DN2=12+（
）2=
，∴CD=
.
故选B.
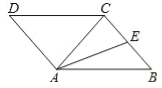
【题目】如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答．
（1）数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
（2）根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系为 ；
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有 条边．
【题目】如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数．
（1）设北京时间为x（时），首尔时间为y（时），就0≤x≤12，求y关于x的函数表达式，并填写下表（同一时刻的两地时间）．
北京时间 | 7：30 | 11：15 | 2：50 |
首尔时间 | 8：30 | 12：15 | 3：50 |
（2）如图2表示同一时刻的英国伦敦时间（夏时制）和北京时间，两地时差为整数．如果现在伦敦（夏时制）时间为7：30，那么此时韩国首尔时间是多少？