Question

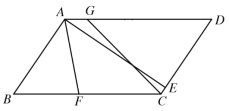
【题目】如图，在平行四边形中，过作于点，点，分别为，上一点，连接交于点，连接，，．

（1）若，，求的长；

（2）求证：．

Answer 1

【答案】（1） ；（2）证明见解析．

【解析】

（1）过H作HP⊥AD交AD于点P，在Rt△PGH中求出PH，在Rt△APH中利用正切求出AP，再利用勾股定理求AH，即可得AF的长；

（2）过点作交于点，过点作交于点K，交AE于点，易得四边形AFKG为平行四边形，得到，然后证明∠AMH=45°=∠GCK，，可证≌，得GC=AM，利用等量代换即可求证结论．

（1）如图，过H作HP⊥AD交AD于点P，

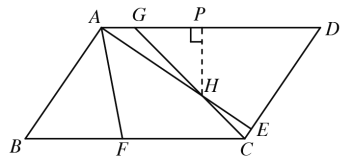
∵在平行四边形中，AD∥BC，∠GCF=45°

∴∠PGH=45°

在Rt△PGH中，GH=4，

∴PH=

在Rt△APH中，

∴

又∵

∴

（2）如图，过点作交于点，过点作交于点K，交AE于点．

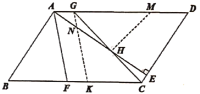
∵AG∥FK，AF∥GK

∴四边形AFKG为平行四边形

∴

由（1）可知∠HGM=45°，

∵HM⊥GH，

∴∠AMH=45°=∠GCK

又∵AF∥GK

∴

∵，

∴

在△GKC和△AHM中，

∵∠GCK=∠AMH，∠CGK=∠MAH，GK=AH，

∴≌（AAS）

∴GC=AM

又∵在等腰Rt△GHM中，GM=GH

∴AM=AG+GM=AG+GH

∴