Question

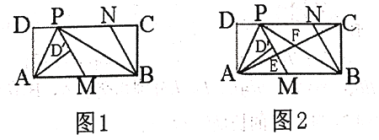
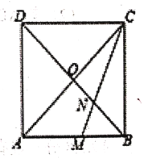
【题目】如图，正方形的对角线与相交于点，的角平分线分别交、于、两点．若,则线段的长为（ ）

A.B.C.1D.

Answer 1

【答案】A

【解析】

过点M作ME⊥AC于E，根据正方形的性质和锐角三角函数即可求出AE=EM=1，△CON∽△CEM，再根据角平分线的性质可得BM=EM=1，从而求出正方形的边长，即可求出对角线AC的长，然后根据相似三角形的性质列出比例式即可求出ON．

解：过点M作ME⊥AC于E

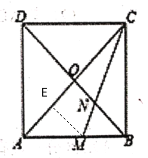
∵正方形的对角线与相交于点

∴∠CAB=45°，∠COB=∠ABC=90°，AB=BC，CO=AO=

∴△AEM为等腰三角形，OB∥EM

∴AE=EM=AM·sin∠EAM=，△CON∽△CEM，

∵CM平分∠ACB

∴BM=EM=1

∴AB=AM＋MB=

在Rt△ABC中，AC=

∴CE=AC－AE=，CO=

∵△CON∽△CEM

∴

即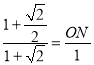

解得：ON=

故选A．