题目内容
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm,动点P从点B开始沿BC边匀速运动,动点Q从点D开始沿对角线DB匀速运动,它们的运动速度均为1cm/s,过点Q作QE⊥CD,与CD交于点E,连接PQ,点P和点Q同时出发,设运动时间为t(s),0<t≤5.
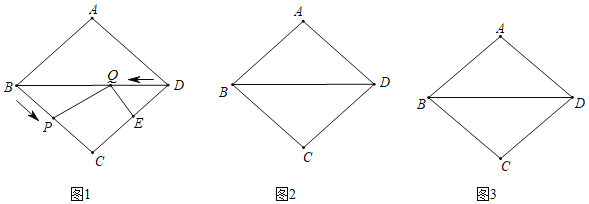
(1)当PQ∥CD时,求t的值;
(2)设四边形PQEC的面积为S(cm2),求S与t之间的函数关系式;
(3)当P,Q两点运动到使∠PQE=60°时,求四边形PQEC的面积;
(4)是否存在某一时刻t,使PQ+QE的值最小?若存在,请求t的值,并求出此时PQ+QE的值;若不存在,请说明理由.
【答案】(1)t=![]() ;(2)S=
;(2)S=![]() t+12;(3)
t+12;(3)![]() ;(4)存在,理由见解析.
;(4)存在,理由见解析.
【解析】
(1)根据平行线分线段成比例定理得:![]() ,代入计算可得t的值;
,代入计算可得t的值;
(2)先根据三角函数表示PH和EQ、DE的长,根据面积差表示S与t之间的函数关系式;
(3)如图2,作辅助线,构建相似三角形和60度的直角三角形,根据平行 线分线段成比例定理列式为:![]() ,可得MQ=BM=
,可得MQ=BM=![]() ,证明△QMP∽△FCP,计算FC的长,根据FE=
,证明△QMP∽△FCP,计算FC的长,根据FE=![]() QE,列方程可得t的值,代入(2)中S与t的关系式可得结论;
QE,列方程可得t的值,代入(2)中S与t的关系式可得结论;
(4)过Q作QF⊥AD于F,当P、Q、F三点共线时,PQ+QE的值最小,最小值就是菱形的高线PF.
解:(1)由题意得:PB=DQ=t,
∵BD=8,
∴BQ=8﹣t,
当PQ∥CD时,![]() ,
,
![]() ,t=
,t=![]() ;
;
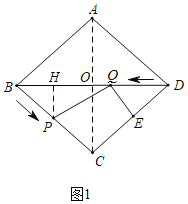
(2)如图1,过P作PH⊥BD于H,连接AC交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BOC=∠COD=90°,
∵AB=BC=CD=5,OB=OD=![]() BD=4,
BD=4,
∴OC=3,
∴sin∠HBP=![]() ,
,
∵PB=t,
∴PH=![]() t,同理得EQ=
t,同理得EQ=![]() ,
,
∴S=S△BCD﹣S△BPQ﹣S△DEQ=![]() ;
;
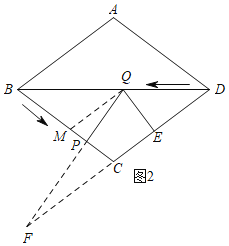
(3)如图2,过Q作QM∥CD,交BC于M,延长QP与EC交于点F,
∴![]() ,即
,即![]() ,
,
∴MQ=BM=![]() ,
,
∴![]() ,
,
∵MQ∥FC,
∴△QMP∽△FCP,
∴![]() ,即
,即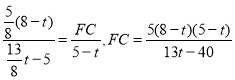 ,
,
Rt△FQE中,∵∠PQE=60°,
![]()
![]()
![]() 由(2)知:四边形PQEC的面积=
由(2)知:四边形PQEC的面积=![]() ,
,
∴四边形PQEC的面积=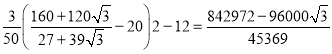 ;
;
(可以过P作CD的平行线);
(4)存在,
如图4,过Q作QF⊥AD于F,
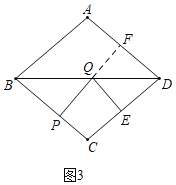
∵四边形ABCD是菱形,
∴BD平分∠ADC,
∵QE⊥CD,
∴QE=QF,
∴当P、Q、F三点共线时,PQ+QE的值最小,
∵AD∥BC,
∴PF⊥BC,
S菱形ABCD=PFBC=![]() ,
,
∵PF=PQ+FQ=PQ+EQ=![]()
∴存在,当t=![]() s时,使PQ+QE的值最小,最小值是
s时,使PQ+QE的值最小,最小值是![]() .
.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案