题目内容
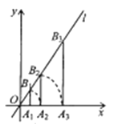
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ,...,按此做法进行下去,则
,...,按此做法进行下去,则![]() 的长是______.
的长是______.
【答案】![]()
【解析】
先根据一次函数方程式求出B1点的坐标,再根据B1点的坐标求出A2点的坐标,得出B2的坐标,以此类推总结规律便可求出点A2020的坐标,再根据弧长公式计算即可求解.
解:直线y=![]() x点A1坐标为(2,0),过点A1作x轴的垂线交 直线于点B1可知B1点的坐标为(2,
x点A1坐标为(2,0),过点A1作x轴的垂线交 直线于点B1可知B1点的坐标为(2,![]() ),
),
以原O为圆心,OB1长为半径画弧x轴于点A2,OA2=OB1
OA2=![]() =4,点A2的坐标为(4,0),
=4,点A2的坐标为(4,0),
这种方法可求得B2的坐标为(4,![]() )故点A3的坐标为(8,0),B3(8,
)故点A3的坐标为(8,0),B3(8,![]() ),
),
以此类推便可求出点A2020的坐标为(22020,0),
则![]() 的长是
的长是![]() =
=![]() .
.
故答案是:![]()

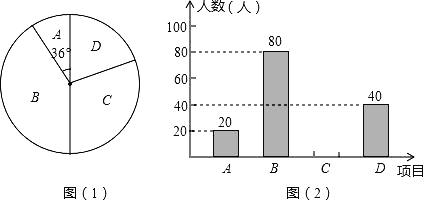
【题目】为了调查某小区居民的用水情况,随机抽查了若干个家庭的![]() 月份用水量,结果如下表:
月份用水量,结果如下表:
月用水量(立方米) |
|
|
|
|
户数 |
|
|
|
|
根据上表解决下列问题:
(1)这组数据的众数是 ,中位数是 ;
(2)求这若干个家庭的![]() 月份平均用水量;
月份平均用水量;
(3)请根据(2)的结论估计该小区![]() 个家庭
个家庭![]() 月份总用水量.
月份总用水量.
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
【题目】在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共![]() 个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
摸球的次数 |
|
|
|
|
|
|
摸到红球的次数 |
|
|
|
|
|
|
摸到红球的频率 |
|
|
|
|
|
|
(1)试估计:盒子中有红球 个;
(2)若从盒子中一次性摸出两个球,用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率.