题目内容
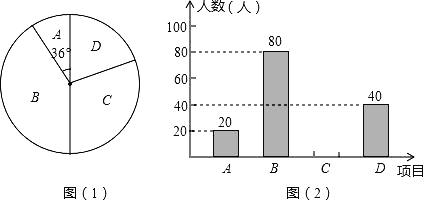
【题目】为了提高学生的综合素质,某中学成立了以下社团:A.机器人,B.围棋,C.羽毛球,D.电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.
根据以上信息,解答下列问题:
(1)这次被调查的学生共有 人,B所占扇形的圆心角是 度;
(2)请你将条形统计图补充完整;
(3)若该校共有1000名学生加人了社团,请你估计这1000名学生中有多少人参加了羽毛球社团;
(4)在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛,用树状图或列表法求恰好选中甲、乙两位同学的概率.
【答案】(1)200;144;(2)见解析;(3)300人;(4)![]()
【解析】
(1)由A类有20人,所占扇形的圆心角为36°,即可求得这次被调查的学生数;用这次被调查的学生数乘以B所占的百分比,即可求得B所占扇形的圆心角;
(2)首先求得C项目对应人数,即可补全统计图;
(3)利用样本估计总体,用该校1000学生数乘以参加了羽毛球社团的人数所占的百分比即可得到结论;
(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.
解:(1)∵A类有20人,所占扇形的圆心角为36°,
∴这次被调查的学生共有:20÷![]() =200(人);
=200(人);
B所占扇形的圆心角是:360°×![]() =144°.
=144°.
故答案为:200,144;
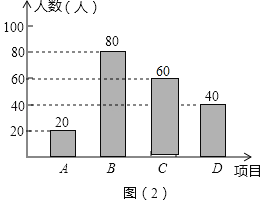
(2)C项目对应人数为:200﹣20﹣80﹣40=60(人);
补充如图.
(3)1000×![]() =300(人).
=300(人).
答:这1000名学生中有300人参加了羽毛球社团;
(4)画树状图得:

∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,
∴P(选中甲、乙)=![]() =
=![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
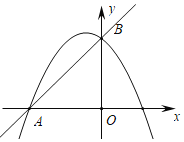
学练快车道口算心算速算天天练系列答案【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )的
)的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
| 0 | 2 |
| 6 | 0 |
|
| 6 |
下列结论:
①![]() ;
;
②当![]() 时,函数最小值为
时,函数最小值为![]() ;
;
③若点![]() ,点
,点![]() 在二次函数图象上,则
在二次函数图象上,则![]() ;
;
④方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)